��Ŀ����
��2011•���������ڡ�ABC�У�AB=CB����ABC=90�㣬FΪAB�ӳ�����һ�㣬��E��BC�ϣ���AE=CF��
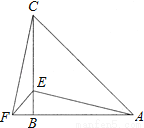
��1����֤��Rt��ABE��Rt��CBF��
��2������CAE=30�㣬���ACF�Ķ�����
 ��1������������2��60�㣮
��������
�����������1����AB=CB����ABC=90�㣬AE=CF����������HL֤��Rt��ABE��Rt��CBF��
��2����AB=CB����ABC=90�㣬������á�CAB���ACB�Ķ��������ɵá�BAE�Ķ���������Rt��ABE��Rt��CBF��������á�BCF�Ķ��������ɡ�ACF=��BCF+��ACB������ô𰸣�
��1��֤�����ߡ�ABC=90�㣬...
��1������������2��60�㣮
��������
�����������1����AB=CB����ABC=90�㣬AE=CF����������HL֤��Rt��ABE��Rt��CBF��
��2����AB=CB����ABC=90�㣬������á�CAB���ACB�Ķ��������ɵá�BAE�Ķ���������Rt��ABE��Rt��CBF��������á�BCF�Ķ��������ɡ�ACF=��BCF+��ACB������ô𰸣�
��1��֤�����ߡ�ABC=90�㣬...
��ͼ����B������AE�ϣ���CBA������AE���ۺ�����SDBA�غϣ�����ȷ���ǣ�����
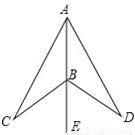
A. CA��DB B. ��CAE=��DBE C. AC=AD D. ��CBA����DBE
 C
���������ߡ�CBA������AE���ۺ������DBA�غϣ�
���D����C����CAB����DAB����CBA����DBA��AC��AD��
��ѡC.
C
���������ߡ�CBA������AE���ۺ������DBA�غϣ�
���D����C����CAB����DAB����CBA����DBA��AC��AD��
��ѡC. ��ͼ��CΪ�߶�AE��һ����(����A��E�غ�)����AEͬ��ֱ�����������ABC����������CDE��AD��BE���ڵ�O��AD��BC���ڵ�P��BE��CD���ڵ�Q������PQ������������ۣ���AD=BE����PQ��AE����AP=BQ����DE=DP���ݡ�AOB=60��.������ȫ��ȷ����___________.
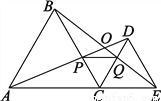
 �٢ڢۢ�
������������������١�ABC�͡�DCE���ǵȱ������Σ���A��C��E��ͬһ��ֱ���ϣ�
��AC=BC,EC=DC,��BCE=��ACD=
���ACD�ա�ECB
��AD=BE���ʱ�ѡ����ȷ��
�ڡߡ�ACD�ա�ECB
���CBQ=��CAP��
�֡ߡ�PCQ=��ACB=CB=AC��
���BCQ�ա�ACP��
��CQ=CP,�֡�PCQ=
���PC...
�٢ڢۢ�
������������������١�ABC�͡�DCE���ǵȱ������Σ���A��C��E��ͬһ��ֱ���ϣ�
��AC=BC,EC=DC,��BCE=��ACD=
���ACD�ա�ECB
��AD=BE���ʱ�ѡ����ȷ��
�ڡߡ�ACD�ա�ECB
���CBQ=��CAP��
�֡ߡ�PCQ=��ACB=CB=AC��
���BCQ�ա�ACP��
��CQ=CP,�֡�PCQ=
���PC... ��ͼ��ʾ,AB-AC=2cm,BC�Ĵ�ֱƽ���߽�AB�ڵ�D,��BC�ڵ�E,��ACD���ܳ���14cm,
��AB��AC�ij�.
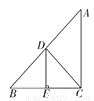
 AB=8,AC=6
����������������������߶δ�ֱƽ�����������BD=DC�������������ܳ����AB+AC=12cm��������֪�ó�AC=AB-2cm����������𰸣�
���������
��DE��ֱƽ��BC,
��BD=CD.
���ACD���ܳ�=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
�ⷽ����
��
��AC=6cm��AB=8cm.
AB=8,AC=6
����������������������߶δ�ֱƽ�����������BD=DC�������������ܳ����AB+AC=12cm��������֪�ó�AC=AB-2cm����������𰸣�
���������
��DE��ֱƽ��BC,
��BD=CD.
���ACD���ܳ�=AD+AC+CD=AD+AC+BD=AB+AC=14cm.
�ⷽ����
��
��AC=6cm��AB=8cm. ��ͼ��ֱ��CD���߶�AB�Ĵ�ֱƽ���ߣ�PΪֱ��CD�ϵ�һ�㣬��֪�߶�PA��5�����߶�PB�ij���Ϊ��������
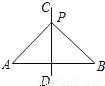
A. 6 B. 5 C. 4 D. 3
 B
����������Ϊ�߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ�����PA=PB����PB=5.
��ѡB.
B
����������Ϊ�߶δ�ֱƽ�����ϵĵ��������߶������˵�ľ�����ȣ�����PA=PB����PB=5.
��ѡB. ������ֱ���������У�����һ�Խ�(��ֱ��)��ȣ�һ�Ա���ȣ�������ֱ��������( )
A. һ��ȫ�� B. һ����ȫ�� C. ��һ��ȫ�� D. ���϶�����
 C
�������������һ�Խ�(��ֱ��)��Ӧ��ȣ�һ�Ա߶�Ӧ��ȣ����л�������һ��ֱ����ȣ���������������һ��ȫ�ȣ�
�����Ƕ�Ӧ��ȣ���һ��ȫ�ȣ�
��ѡC.
C
�������������һ�Խ�(��ֱ��)��Ӧ��ȣ�һ�Ա߶�Ӧ��ȣ����л�������һ��ֱ����ȣ���������������һ��ȫ�ȣ�
�����Ƕ�Ӧ��ȣ���һ��ȫ�ȣ�
��ѡC. ���и��������У����ж�����ֱ��������ȫ�ȵ���( )
A. һ��߶�Ӧ��� B. ����ֱ�DZ߶�Ӧ���
C. ������Ƕ�Ӧ��� D. һ����Ƕ�Ӧ���
 B
��������A����ֱ������������һ����������ֱ����ȣ�����֪һ��߶�Ӧ��� ��Ҫ�ж���ֱ��������ȫ�ȣ�����Ҫһ��Ƕ�Ӧ��ȵػ�����һ��߶�Ӧ��Ȳ��ܽ����ж�����ѡ�����
B���������ñ߽DZ��ж���������ȫ�ȣ��ʱ�ѡ����ȷ��
C��������Ƿֱ���ȣ�ֻ�н�û�бߣ������ж�ȫ�ȣ���ѡ�����
D��һ����Ƕ�Ӧ��ȣ�����һ����������ֱ����ȣ����ݽǶ�Ӧ��ȣ������ж�������ȫ�ȣ���ѡ...
B
��������A����ֱ������������һ����������ֱ����ȣ�����֪һ��߶�Ӧ��� ��Ҫ�ж���ֱ��������ȫ�ȣ�����Ҫһ��Ƕ�Ӧ��ȵػ�����һ��߶�Ӧ��Ȳ��ܽ����ж�����ѡ�����
B���������ñ߽DZ��ж���������ȫ�ȣ��ʱ�ѡ����ȷ��
C��������Ƿֱ���ȣ�ֻ�н�û�бߣ������ж�ȫ�ȣ���ѡ�����
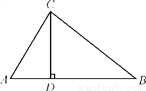
D��һ����Ƕ�Ӧ��ȣ�����һ����������ֱ����ȣ����ݽǶ�Ӧ��ȣ������ж�������ȫ�ȣ���ѡ... ��ͼ���ڡ�ABC�У�CD��AB������Ϊ��D.��AB��12��CD��6��tanA��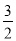 ����sinB��cosB��ֵ��
����sinB��cosB��ֵ��
 .
���������������������Rt��ACD�У������к����Ķ����tanA==�����AD=4����BD=AB��AD=8���ٽ�Rt��BCD���ɹ��ɶ�����BC==10��sinB==��cosB==���ɴ����sinB+cosB=��
��������
��Rt��ACD�У��ߡ�ADC=90�㣬
��tanA===��
��AD=4��
��BD=AB��AD=12��4=8��
��Rt��BCD�У��ߡ�BD...
.
���������������������Rt��ACD�У������к����Ķ����tanA==�����AD=4����BD=AB��AD=8���ٽ�Rt��BCD���ɹ��ɶ�����BC==10��sinB==��cosB==���ɴ����sinB+cosB=��
��������
��Rt��ACD�У��ߡ�ADC=90�㣬
��tanA===��
��AD=4��
��BD=AB��AD=12��4=8��
��Rt��BCD�У��ߡ�BD... ��ͼ��ֱ��AB��CD�ཻ�ڵ�O��OBƽ�֡�DOE������DOE=60�㣬���AOC�Ķ�����_____.
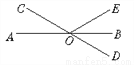
 30��
����������Ϊ��BOD=45�㣬���ԡ�AOC=��BOD=45�㣨�Զ�����ȣ�����ΪOE��AB�����AOE=90�㣬���ԡ�COE=��COA+��AOE=45��+90��=135��.
30��
����������Ϊ��BOD=45�㣬���ԡ�AOC=��BOD=45�㣨�Զ�����ȣ�����ΪOE��AB�����AOE=90�㣬���ԡ�COE=��COA+��AOE=45��+90��=135��. 
