��Ŀ����
����˵����:
��P���߶�AB�ϵ�һ��,ֱ��l������P��l��AB,��l���߶�AB�Ĵ�ֱƽ����;
��ֱ��l�����߶�AB���е�,��l���߶�AB�Ĵ�ֱƽ����;
����AP=PB,��ֱ��l��ֱ���߶�AB,��l���߶�AB�Ĵ�ֱƽ����;
�ܾ����߶�AB���е�P�Ҵ�ֱ��AB��ֱ��l���߶�AB�Ĵ�ֱƽ����.
������ȷ����(����)
A. 1�� B. 2�� C. 3�� D. 4��
 A
�������������߶εĴ�ֱƽ���ߵĶ��壬�Լ����������߶ε����˾�����ȵĵ����߶εĴ�ֱƽ�����ϣ������жϣ�
��������
�ٵ�P����AB���е㣬��ֱ��l��ƽ���߶�AB���ʴ���
��ֱ��l�����߶�AB���е㣬�Ҵ�ֱ��AB��l���߶�AB�Ĵ�ֱƽ���ߣ��ʴ���
����AP=PB����P���߶�AB�Ĵ�ֱƽ�����ϣ���l��һ������P������ֱ��l��һ�����߶�AB�Ĵ�ֱƽ���ߣ��ʴ���
��...
A
�������������߶εĴ�ֱƽ���ߵĶ��壬�Լ����������߶ε����˾�����ȵĵ����߶εĴ�ֱƽ�����ϣ������жϣ�
��������
�ٵ�P����AB���е㣬��ֱ��l��ƽ���߶�AB���ʴ���
��ֱ��l�����߶�AB���е㣬�Ҵ�ֱ��AB��l���߶�AB�Ĵ�ֱƽ���ߣ��ʴ���
����AP=PB����P���߶�AB�Ĵ�ֱƽ�����ϣ���l��һ������P������ֱ��l��һ�����߶�AB�Ĵ�ֱƽ���ߣ��ʴ���
��...
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�������ͼ��ȫ�ȣ�������һ��ͼ�ο�ͨ��ƽ�ơ�__________��__________����һ����������ȫ�غ�.
 ��ת �Գ�
��������һ��ͼ�ξ�����ת���Գơ����ۺ��ı�ͼ�ε���״���С��������ԭͼ����ȫ�ȵģ�
����������ͼ��ȫ�ȣ�������һ��ͼ�ο�ͨ��ƽ�ơ���ת��Գ�����һ����������ȫ�غϣ�
�ʴ�Ϊ����ת���Գ�.
��ת �Գ�
��������һ��ͼ�ξ�����ת���Գơ����ۺ��ı�ͼ�ε���״���С��������ԭͼ����ȫ�ȵģ�
����������ͼ��ȫ�ȣ�������һ��ͼ�ο�ͨ��ƽ�ơ���ת��Գ�����һ����������ȫ�غϣ�
�ʴ�Ϊ����ת���Գ�. ��ͼ����֪�ڡ�ABC�У�AD��BC�ڵ�D��AEƽ�֡�BAC���жϡ�EAD��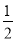 (��C����B)�Ĺ�ϵ����˵�����ɣ�
(��C����B)�Ĺ�ϵ����˵�����ɣ�
 ��EAD= (��C����B)�����ɼ�����
����������������������������ڽǺͶ�����������DAC�͡�EAC��������ɵó��𰸣�
���������
�����ǣ�
��AEƽ�֡�BAC��
��AD��BC��
��EAD= (��C����B)�����ɼ�����
����������������������������ڽǺͶ�����������DAC�͡�EAC��������ɵó��𰸣�
���������
�����ǣ�
��AEƽ�֡�BAC��
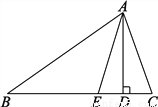
��AD��BC�� ��ͼ�����ı���ABCD�У�AD��BC��EΪCD���е㣬����AE��BE��BE��AE���ӳ�AE��BC���ӳ����ڵ�F��
��֤����1��FC��AD��
��2��AB��BC��AD��
 ��1��֤������������2��֤��������.
���������������:��1������AD��BC��֪��ADC=��ECF���ٸ���E��CD���е�������ADE�ա�FCE������ȫ�������ε����ʼ��ɽ��
��2�������߶δ�ֱƽ���ߵ������жϳ�AB=BF���ɣ�
֤������1����AD��BC����֪����
���ADC=��ECF����ֱ��ƽ�У��ڴ�����ȣ���
��E��CD���е㣨��֪����
��DE=EC���е�...
��1��֤������������2��֤��������.
���������������:��1������AD��BC��֪��ADC=��ECF���ٸ���E��CD���е�������ADE�ա�FCE������ȫ�������ε����ʼ��ɽ��
��2�������߶δ�ֱƽ���ߵ������жϳ�AB=BF���ɣ�
֤������1����AD��BC����֪����
���ADC=��ECF����ֱ��ƽ�У��ڴ�����ȣ���
��E��CD���е㣨��֪����
��DE=EC���е�... ��ABC�У�AB = 5��AC = 6��BC = 4����AB�Ĵ�ֱƽ���߽�AC�ڵ�D�����BDC���ܳ��ǣ� ��
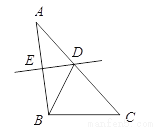
A. 8 B. 9 C. 10 D. 11
 C
�������������������ED��AB�Ĵ�ֱƽ���ߣ��ɵ�AD=BD�����ɡ�BDC���ܳ�=DB+BC+CD�����ɵá�BDC���ܳ�=AD+BC+CD=AC+BC�� ��ED��AB�Ĵ�ֱƽ���ߣ� ��AD=BD��
�ߡ�BDC���ܳ�=DB+BC+CD�� ���BDC���ܳ�=AD+BC+CD=AC+BC=6+4=10��
C
�������������������ED��AB�Ĵ�ֱƽ���ߣ��ɵ�AD=BD�����ɡ�BDC���ܳ�=DB+BC+CD�����ɵá�BDC���ܳ�=AD+BC+CD=AC+BC�� ��ED��AB�Ĵ�ֱƽ���ߣ� ��AD=BD��
�ߡ�BDC���ܳ�=DB+BC+CD�� ���BDC���ܳ�=AD+BC+CD=AC+BC=6+4=10�� ��ͼ,��ABC,��CDE��Ϊ����ֱ��������,��ACB=��DCE=90��,��E��AB��,��˵��:��CDA�ա�CEB.
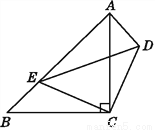
 �𰸼�����
��������������������ݵ���ֱ�������ε����ʵó�CE=CD��BC=AC��������ȫ�������ε��ж�֤�����ɣ�
���������֤�����ߡ�ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬
��CE=CD��BC=AC��
���ACB����ACE=��DCE����ACE��
���ECB=��DCA��
�ڡ�CDA���CEB�У� ��
���CDA�ա�CEB��
�𰸼�����
��������������������ݵ���ֱ�������ε����ʵó�CE=CD��BC=AC��������ȫ�������ε��ж�֤�����ɣ�
���������֤�����ߡ�ABC����CDE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬
��CE=CD��BC=AC��
���ACB����ACE=��DCE����ACE��
���ECB=��DCA��
�ڡ�CDA���CEB�У� ��
���CDA�ա�CEB�� ��ͼ��ʾ����Rt��ACD��Rt��BCE�У���AD��BE��DC��EC�������ó��Ľ�����( )

A. OA��OB B. E��AC���е� C. ��AOE�ա�BOD D. AE��BD
 B
���������ߡ�C=��C=90�㣬
���ACD�͡�BCE��ֱ�������Σ�
��Rt��ACD��Rt��BCE��
��Rt��ACD��Rt��BCE��HL����
���B=��A��CB=CA��
��CD=CE��
��AE=BD����D��ȷ��
�ڡ�AOE�͡�BOD�У�
���AOE�ա�BOD��AAS������C��ȷ��
��AO=OB����A��ȷ��
AE=BD��CE=CD...
B
���������ߡ�C=��C=90�㣬
���ACD�͡�BCE��ֱ�������Σ�
��Rt��ACD��Rt��BCE��
��Rt��ACD��Rt��BCE��HL����
���B=��A��CB=CA��
��CD=CE��
��AE=BD����D��ȷ��
�ڡ�AOE�͡�BOD�У�
���AOE�ա�BOD��AAS������C��ȷ��
��AO=OB����A��ȷ��
AE=BD��CE=CD... �Ķ�����IJ��ϣ��ٻش����⣺
���Ǻ����г��ù�ʽsin(A��B)��sinAcosB��cosAsinB����sin(A��B)��ֵ��
���磺sin75�㣽sin(45�㣫30��)��sin45��cos30�㣫cos45��sin30�㣽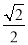 ��
��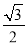 ��
��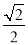 ��
��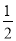 ��
��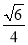 ��
��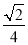 ��
��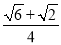 .
.
���ù�ʽcos(A��B)��cosAcosB��sinAsinB����cos75���ֵ��
 �������������������cos75���Ϊcos(45��+30��)��Ȼ�������Ĺ�ʽ���м��㼴��.
���������cos75�㣽cos(45�㣫30��)��cos45��cos30�㣭sin45��sin30��=.
�������������������cos75���Ϊcos(45��+30��)��Ȼ�������Ĺ�ʽ���м��㼴��.
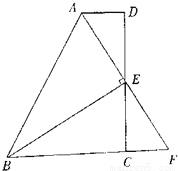
���������cos75�㣽cos(45�㣫30��)��cos45��cos30�㣭sin45��sin30��=. ��ͼ����l1��l2����1=45�㣬���2=_____.
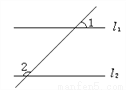
 135
��������������������ݶԶ��ǵ����������1�ĶԶ��ǣ�Ȼ�������ֱ��ƽ��ͬ���ڽǻ����ó���2�Ķ���.
135
��������������������ݶԶ��ǵ����������1�ĶԶ��ǣ�Ȼ�������ֱ��ƽ��ͬ���ڽǻ����ó���2�Ķ���. 
