已知在Rt△ABC中，∠C=90°，AC=4，cotA=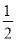
，则BC的长是 ．
8
【解析】
试题分析：如图所示：
∵在Rt△ABC中，∠C=90°，AC=4，cotA=，
∴cotA==，
∴BC=8． 如图，在建筑平台CD的顶部C处，测得大树AB的顶部A的仰角为45°，测得大树AB的底部B的俯角为30°，已知平台CD的高度为5m，则大树的高度为 m（结果保留根号）
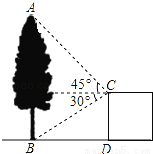
5+5.
【解析】
试题分析：作CE⊥AB于点E，
在Rt△BCE中，
BE=CD=5m，
CE==5m，
在Rt△ACE中，
AE=CE•tan45°=5m，
AB=BE+AE=（5+5）m． 计算：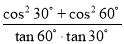 
+sin45°．
【解析】
试题分析：根据特殊角的三角函数值，可得实数的运算，根据实数的运算，可得答案．
试题解析：+sin45°
=
=2+
= 计算：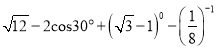 
．
．
【解析】试题分析：分别进行二次根式的化简、特殊角的三角函数值、零指数幂、负整数指数幂等运算，然后按照实数的运算法则计算即可．
试题解析：原式=
=． 在Rt△ABC中，∠C=90°，a=8，∠B=60°，解这个直角三角形．
∠A=30°，AB=16，AC=
【解析】试题分析：根据三角形内角和定理求出∠A，根据含30度角直角三角形求出AB，根据勾股定理求出AC即可．
试题解析：∵∠C=90°，∠B=60°，
∴∠A=180°-∠C-∠B=30°，
∵BC=a=8，
∴AB=2a=16，
由勾股定理得：AC= ． 如图所示，某船上午11时30分在A处观测海岛B在北偏东60°方向，该船以每小时10海里的速度航行到C处，再观测海岛B在北偏东30°方向，又以同样的速度继续航行到D处，再观测海岛在北偏西30°方向，当轮船到达C处时恰好与海岛B相距20海里，请你确定轮船到达C处和D处的时间．
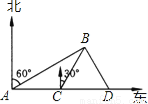
轮船到达C处的时间为13时30分，到达D处的时间15时30分
【解析】试题分析：首先根据题意得出∠BAC=30°，∠BCD=60°，从而得出∠BAC=∠CBA=30°，则AC=BC，根据题意得出∠BDC=60°，得到△BCD为等边三角形，则BC=AC=CD=BD=20，从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析：∵在A处观测海岛B在北偏东60°方向，∴∠... 小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同．此时，测得小明落在墙上的影子高度CD＝1.2m，CE＝0.8m，CA＝30m（点A、E、C在同一直线上）．已知小明的身高EF是1.7m，请你帮小明求出楼高AB（结果精确到0.1m）．
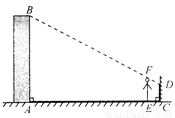
20.0米．
【解析】试题分析：此题属于实际应用问题，解题的关键是将实际问题转化为数学问题进行解答；解题时要注意构造相似三角形，利用相似三角形的性质解题．
试题解析：如图：过点D作DG⊥AB，分别交AB、EF于点G、H，∵AB∥CD，DG⊥AB，AB⊥AC，∴四边形ACDG是矩形，∴EH=AG=CD=1.2，DH=CE=0.8，DG=CA=30，∵EF∥AB，∴，由题意，知FH=EF﹣... 如图，在一次数学课外实践活动中，要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD，测得教学楼顶端A的仰角为30°，然后向教学楼前进40m到达E，又测得教学楼顶端A的仰角为60°．求这幢教学楼的高度AB．
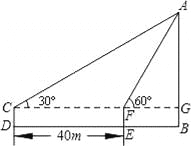
米
【解析】试题分析：首先根据Rt△AFG中∠AFG的正切值得出FG的长度，然后根据∠ACG的正切得出CG的长度，然后根据CG－FG=40得出AG的长度，从而得出AB的长度.
试题解析：在Rt△AFG中，tan∠AFG=∴FG=
在Rt△ACG中， tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答：这幢教学楼的高度AB为... 如图1，小红家阳台上放置了一个晒衣架．如图2是晒衣架的侧面示意图，立杆AB、CD相交于点O，B、D两点立于地面，经测量：AB=CD=136cm，OA=OC=51cm，OE=OF=34cm，现将晒衣架完全稳固张开，扣链EF成一条直线，且EF=32cm．
（1）求证：AC∥BD；
（2）求扣链EF与立杆AB的夹角∠OEF的度数（精确到0.1°）；
（3）小红的连衣裙穿在衣架后的总长度达到122cm，垂挂在晒衣架上是否会拖落到地面？请通过计算说明理由．
（参考数据：sin61.9°≈0.882，cos61.9°≈0.471，tan61.9°≈0.553；可使用科学计算器）
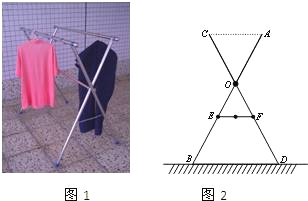
（1）证明参见解析；(2) 61.9°；(3) 小红的连衣裙会拖落到地面．理由参见解析.
【解析】
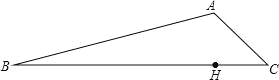
试题分析：（1）根据等角对等边和对顶角相等得出∠OAC=∠OCA=（180º-∠AOC）和∠OBD=∠ODB=（180º-∠BOD），∠AOC=∠BOD进而利用平行线的判定得出即可；或利用三角形相似和平行线判定可得出结论；（2）首先过点O作OM⊥EF于点M，则EM=16cm，利用cos∠... 如图，现有甲、乙两个小分队分别同时从B、C两地出发前往A地，甲沿线路BA行进，乙沿线路CA行进，已知C在A的南偏东55°方向，AB的坡度为1：5，同时由于地震原因造成BC路段泥石堵塞，在BC路段中位于A的正南方向上有一清障处H，负责抢修BC路段，已知BH为12000m．
（1）求BC的长度；
（2）如果两个分队在前往A地时匀速前行，且甲的速度是乙的速度的三倍．试判断哪个分队先到达A地．（tan55°≈1.4，sin55°≈0.84，cos55°≈0.6，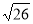
≈5.01，结果保留整数）
(1)、15360m；(2)、乙
【解析】
试题分析：(1)、利用坡度的定义得出AH的长，再利用tan∠HAC=，得出CH的长，进而得出答案；(2)、利用勾股定理得出AB的长利用cos∠HAC=，得出AC的长进而得出答案．
试题解析：(1)、连接AH ∵H在A的正南方向， ∴AH⊥BC， ∵AB的坡度为：1：5，
∴在Rt△ABH中， =， ∴AH=12000×=2400（...