题目内容
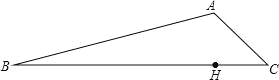
如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
(1)求BC的长度;
(2)如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6,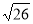 ≈5.01,结果保留整数)
≈5.01,结果保留整数)
 (1)、15360m;(2)、乙
【解析】
试题分析:(1)、利用坡度的定义得出AH的长,再利用tan∠HAC=,得出CH的长,进而得出答案;(2)、利用勾股定理得出AB的长利用cos∠HAC=,得出AC的长进而得出答案.
试题解析:(1)、连接AH ∵H在A的正南方向, ∴AH⊥BC, ∵AB的坡度为:1:5,
∴在Rt△ABH中, =, ∴AH=12000×=2400(...
(1)、15360m;(2)、乙
【解析】
试题分析:(1)、利用坡度的定义得出AH的长,再利用tan∠HAC=,得出CH的长,进而得出答案;(2)、利用勾股定理得出AB的长利用cos∠HAC=,得出AC的长进而得出答案.
试题解析:(1)、连接AH ∵H在A的正南方向, ∴AH⊥BC, ∵AB的坡度为:1:5,
∴在Rt△ABH中, =, ∴AH=12000×=2400(...
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
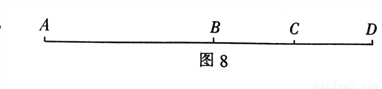
小学生10分钟应用题系列答案如图,点ABCD在同一条线段上,已知BC=6cm,AC=3CD,且点C是BD的中点。求BD和AC的长。请补全以下解答过程
【解析】
因为BC=6cm,且点C是BD的中点,
所以BD= = cm所以CD= cm
又因为AC=3CD,所以AC= cm
 2BC、12、6、18
【解析】试题分析:根据线段中点的定义可知BD=2BC,代入BC 的长即可求出BD的长,然后根据CD=BD-BC即可求出CD的长;直接将CD的长代入AC=3CD即可得出答案.
试题解析:
【解析】
因为BC=6cm,且点C是BD的中点,
所以BD=2BC=12cm,
所以CD=BD-BC=6cm,
又因为AC=3CD,
所以AC=1...
2BC、12、6、18
【解析】试题分析:根据线段中点的定义可知BD=2BC,代入BC 的长即可求出BD的长,然后根据CD=BD-BC即可求出CD的长;直接将CD的长代入AC=3CD即可得出答案.
试题解析:
【解析】
因为BC=6cm,且点C是BD的中点,
所以BD=2BC=12cm,
所以CD=BD-BC=6cm,
又因为AC=3CD,
所以AC=1... 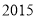 年
年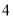 月,生物学家发现一种病毒的长度约为
月,生物学家发现一种病毒的长度约为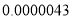 米,将
米,将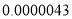 用科学记数法可表示
用科学记数法可表示
为( ).
A. 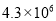 B.
B. 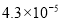 C.
C. 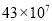 D.
D. 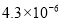
 D
【解析】试题解析: 用科学记数法可表示为: .
故选D.
D
【解析】试题解析: 用科学记数法可表示为: .
故选D. 某商店举办有奖销售活动,办法如下:凡购物满100元者得奖券一张,多购多得,每10000张奖券为一个开奖单位,设立特等奖1个,一等奖50个,二等奖100个,那么买100元商品的中奖概率是( )
A. 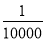 B.
B. 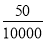 C.
C. 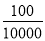 D.
D. 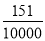
 D
【解析】每10000张奖券为一个开奖单位,共有奖:特等奖1个+一等奖50个+二等奖100个=151个奖,所以买100元商品的中奖的概率是,故选D.
D
【解析】每10000张奖券为一个开奖单位,共有奖:特等奖1个+一等奖50个+二等奖100个=151个奖,所以买100元商品的中奖的概率是,故选D. 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1, 在乙种地板上最终停留在黑色区域的概率为P2, 则( )
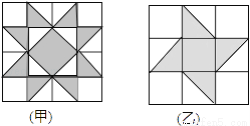
A. P1>P2 B. P1<P2 C. P1=P2 D. 以上都有可能
 A
【解析】试题分析:根据题意可知: ,则,故选A.
A
【解析】试题分析:根据题意可知: ,则,故选A. 在Rt△ABC中,∠C=90°,a=8,∠B=60°,解这个直角三角形.
 ∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
由勾股定理得:AC= .
∠A=30°,AB=16,AC=
【解析】试题分析:根据三角形内角和定理求出∠A,根据含30度角直角三角形求出AB,根据勾股定理求出AC即可.
试题解析:∵∠C=90°,∠B=60°,
∴∠A=180°-∠C-∠B=30°,
∵BC=a=8,
∴AB=2a=16,
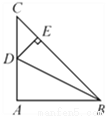
由勾股定理得:AC= . 如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
A. 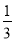 B.
B. 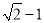 C.
C. 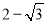 D.
D. 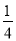
 A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A.
A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A. 如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是____________
 a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5.
a>5
【解析】因为?2<2<5,所以a?2< a+2< a+5,
所以由三角形三边关系可得a?2+a+2>a+5,解得a>5. 如图,ΔABC≌ΔCDA,∠BAC=∠DCA,则BC的对应边是 ( )
A. CD B. CA C. DA D. AB
 C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C.
C
【解析】∵ΔABC≌ΔCDA,∠BAC=∠DCA,
∴BC的对应边为DA,
故选C. 
