题目内容
计算: 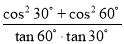 +sin45°.
+sin45°.
 【解析】
试题分析:根据特殊角的三角函数值,可得实数的运算,根据实数的运算,可得答案.
试题解析:+sin45°
=
=2+
=
【解析】
试题分析:根据特殊角的三角函数值,可得实数的运算,根据实数的运算,可得答案.
试题解析:+sin45°
=
=2+
=
某校组织七年级学生参加社会实践活动,若租用45座的客车a辆,则余下的15人无座位;若租用60座的客车则可以少租用1辆,且最后一辆车还有空余的座位,那么乘坐最后一辆60座客车的学生数是( )
A. 75-15a B. 135-15a C. 75+15a D. 135-60a
 B
【解析】试题分析:总人数为:45a+15,
则最后一辆车的人数为:45a+15-60(a-2)=135-15a.
故选B.
B
【解析】试题分析:总人数为:45a+15,
则最后一辆车的人数为:45a+15-60(a-2)=135-15a.
故选B. 数学试卷的选择题都是四选一的单项选择题,小明对某道选择题完全不会做,只能靠猜测获得结果,则小明答对的概率是_____.
 【解析】因为选择题有四个选项,所以小明靠猜测获得结果,其答对的概率是.故答案为: .
【解析】因为选择题有四个选项,所以小明靠猜测获得结果,其答对的概率是.故答案为: . 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1, 在乙种地板上最终停留在黑色区域的概率为P2, 则( )
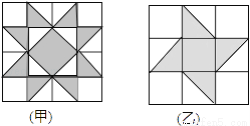
A. P1>P2 B. P1<P2 C. P1=P2 D. 以上都有可能
 A
【解析】试题分析:根据题意可知: ,则,故选A.
A
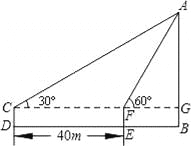
【解析】试题分析:根据题意可知: ,则,故选A. 如图,在一次数学课外实践活动中,要求测教学楼的高度AB、小刚在D处用高1.5m的测角仪CD,测得教学楼顶端A的仰角为30°,然后向教学楼前进40m到达E,又测得教学楼顶端A的仰角为60°.求这幢教学楼的高度AB.
 米
【解析】试题分析:首先根据Rt△AFG中∠AFG的正切值得出FG的长度,然后根据∠ACG的正切得出CG的长度,然后根据CG-FG=40得出AG的长度,从而得出AB的长度.
试题解析:在Rt△AFG中,tan∠AFG=∴FG=
在Rt△ACG中, tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答:这幢教学楼的高度AB为...
米
【解析】试题分析:首先根据Rt△AFG中∠AFG的正切值得出FG的长度,然后根据∠ACG的正切得出CG的长度,然后根据CG-FG=40得出AG的长度,从而得出AB的长度.
试题解析:在Rt△AFG中,tan∠AFG=∴FG=
在Rt△ACG中, tan∠ACG=∴CG=又CG-FG=40
即AG-=40 ∴AG=20∴AB=20+1.5
答:这幢教学楼的高度AB为... 如图,在△ABC 中,∠BAC=90°,AB=AC,点 D 为边AC 的中点,DE⊥BC 于点E,连接BD,则tan∠DBC 的值为 ( )
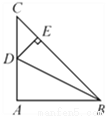
A. 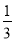 B.
B. 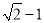 C.
C. 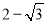 D.
D. 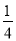
 A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A.
A
【解析】试题分析:∵在△ABC中,∠BAC=Rt∠,AB=AC,∴∠ABC=∠C=45°,BC=AC,又∵点D为边AC的中点,∴AD=DC=AC,∵DE⊥BC于点E,∴∠CDE=∠C=45°,∴DE=EC=DC=AC,∴tan∠DBC===.故选A. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值
A. 也扩大3倍 B. 缩小为原来的
C. 都不变 D. 有的扩大,有的缩小
 C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C.
C
【解析】试题分析:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.
故选C. 如图:(1)AD⊥BC,垂足为D,则AD是__的高,∠__=∠__=90°;
(2)AE平分∠BAC,交BC于点E,则AE叫__,∠__=∠__=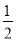 ∠__,AH叫__;
∠__,AH叫__;
(3)若AF=FC,则△ABC的中线是__;
(4)若BG=GH=HF,则AG是__的中线,AH是__的中线.
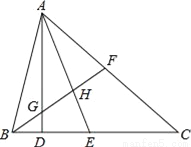
 BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线...
BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析:(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线;
(3)若AF=FC,则△ABC的中线是BF;
(4)若BG=GH=HF,则AG是△ABH的中线... 下列图形能分成两个全等图形的是()
A. 
B. 
C. 
D. 
 C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C.
C
【解析】全等图形需要大小相等,形状相同,原图中只有C是一个等腰三角形可以分成两个全等的直角三角形,A、B、D都不符合要求,
故选C. 
