题目内容
在Rt△ABC中，∠C=90°，a=8，∠B=60°，解这个直角三角形．
∠A=30°，AB=16，AC=
【解析】试题分析：根据三角形内角和定理求出∠A，根据含30度角直角三角形求出AB，根据勾股定理求出AC即可．
试题解析：∵∠C=90°，∠B=60°，
∴∠A=180°-∠C-∠B=30°，
∵BC=a=8，
∴AB=2a=16，
由勾股定理得：AC= ．
新题型全程检测期末冲刺100分系列答案在0.5，-0.5和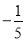
这三个数中，最小的数是______
-0.5
【解析】试题分析：0.5＞＞－0.5，
所以最小的数是－0.5．
故答案为：－0.5． 请将下列事件发生的概率标在图中：
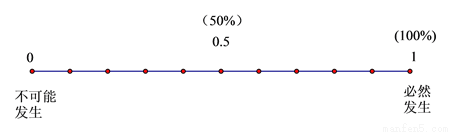
（1）随意掷两枚质地均匀的骰子，朝上面的点数之和为1；
（2）抛出的篮球会下落；
（3）从装有3个红球、7个白球的口袋中任取一个球，恰好是红球（这些球除颜色外完全相同）；
见解析
【解析】分析：本题考察对概率意义的理解，关键是根据各小题题干，分析出概率是多少.
本题解析:
（1）因为每一枚质地均匀的骰子，抛掷后朝上面的点数最小为1，所以两枚朝上面的点数之和最小为2，因此，点数之和为1是不可能发生的.
（2）在地球万有引力的作用下，抛出的篮球会下落，这是必然发生的.所以可能性为1.
（3）口袋中装有3个红球、7个白球，共有10个球，任取一... 一个事件的概率不可能是（ ）
A. 0 B.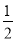 
C. 1 D.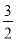 
D
【解析】一个事件的概率不可能是.
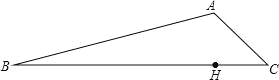
故选D. 如图，现有甲、乙两个小分队分别同时从B、C两地出发前往A地，甲沿线路BA行进，乙沿线路CA行进，已知C在A的南偏东55°方向，AB的坡度为1：5，同时由于地震原因造成BC路段泥石堵塞，在BC路段中位于A的正南方向上有一清障处H，负责抢修BC路段，已知BH为12000m．
（1）求BC的长度；
（2）如果两个分队在前往A地时匀速前行，且甲的速度是乙的速度的三倍．试判断哪个分队先到达A地．（tan55°≈1.4，sin55°≈0.84，cos55°≈0.6，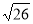
≈5.01，结果保留整数）
(1)、15360m；(2)、乙
【解析】
试题分析：(1)、利用坡度的定义得出AH的长，再利用tan∠HAC=，得出CH的长，进而得出答案；(2)、利用勾股定理得出AB的长利用cos∠HAC=，得出AC的长进而得出答案．
试题解析：(1)、连接AH ∵H在A的正南方向， ∴AH⊥BC， ∵AB的坡度为：1：5，
∴在Rt△ABH中， =， ∴AH=12000×=2400（... 如图所示，四边形ABCD中，∠B=90°，AB=2，CD=8，AC⊥CD，若sin∠ACB=
，则cos∠ADC= ．
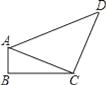
【解析】试题分析：首先在△ABC中，根据三角函数值计算出AC=，再利用勾股定理计算出AD=10，然后根据余弦定义可算出cos∠ADC=． 一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图所示，则下列关系或结论错误的是( )
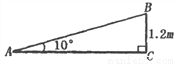
A. 斜坡AB的坡角是10° B. 斜坡AB的坡度是tan10° C. AC=1.2tan10°米 D. AB=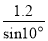
米
C
【解析】根据题意及图形可知： 斜坡AB的坡角是10°，斜坡AB的坡度是tan10°， AC= 米， AB=米，
故错误的是C，
故选C. 如图，△ABC中，∠ABC、∠ACB的平分线相交于点I．
（1）若∠ABC=70°，∠ACB=50°，则∠BIC=__；
（2）若∠ABC+∠ACB=120°，则∠BIC=__；
（3）若∠A=60°，则∠BIC=__；
（4）若∠A=100°，则∠BIC=__；
（5）若∠A=n°，则∠BIC=__．
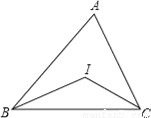
120° 120°， 120° 140°， 90°+n°．
【解析】试题解析：(1)∵BI是∠ABC的平分线，
∵CI是∠ACB的平分线，
在△BCI中，
(2)∵BI是∠ABC的平分线，CI是∠ACB的平分线，
在△BCI中，
(3)在△ABC中，
∵BI是∠ABC的平分线，CI是∠ACB的平分线，
在△BCI中，
(4)在△ABC中，
... 下列说法正确的是（ ）.
A．所有正方形都是全等图形
B．面积相等的两个三角形是全等图形
C．所有半径相等的圆都是全等图形
D．所有长方形都是全等图形
C．
【解析】
试题分析：根据全等图形的定义进行判断. A、所有正方形不一定是全等图形，故此选项错误；B、面积相等的两三角形不一定全等，故此选项错误；C、所有半径相等的圆都是全等图形，故此选项正确；D、所有长方形不一定是全等图形，故此选项错误．
故选：C．