题目内容
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
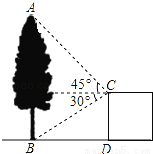
 5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m.
5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m.
下列关于x的方程变形中,正确的是( )
A. 方程3x-2=2x+1,移项,得3x-2x=-1+2
B. 方程3-x=2-5(x-1),去括号,得3-x=2-5x-1
C. 方程3x=2,系数化为1,得x=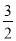
D. 方程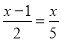 ,去分母,得5(x-1)=2x
,去分母,得5(x-1)=2x
 D
【解析】试题分析:A、方程3x-2=2x+1,移项,得3x-2x=1+2,故此选项错误;
B、方程3-x=2-5(x-1),去括号,得3-x=2-5x+5,故此选项错误;
C、方程3x=2,系数化为1,得x=,故此选项错误;
D、方程,去分母,得5(x-1)=2x,故此选项正确.
故选D.
D
【解析】试题分析:A、方程3x-2=2x+1,移项,得3x-2x=1+2,故此选项错误;
B、方程3-x=2-5(x-1),去括号,得3-x=2-5x+5,故此选项错误;
C、方程3x=2,系数化为1,得x=,故此选项错误;
D、方程,去分母,得5(x-1)=2x,故此选项正确.
故选D. 任意掷一枚质地均匀的骰子,朝上的点数是奇数的概率是______.
 【解析】任意掷一枚质地均匀的骰子,朝上的点数可能是1,2,3,4,5,6,其中有三个奇数,因此朝上的点数是奇数的概率是.故答案为: .
【解析】任意掷一枚质地均匀的骰子,朝上的点数可能是1,2,3,4,5,6,其中有三个奇数,因此朝上的点数是奇数的概率是.故答案为: . 一个袋中装有2个红球,3个蓝球和5个白球,它们除颜色外完全相同,现在从中任意摸出一个球,则P(摸到红球)等于( )
A. 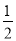 B.
B. 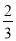 C.
C. 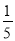 D.
D. 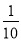
 C
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C.
C
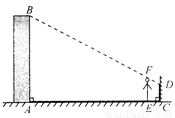
【解析】袋中有2个红球,3个蓝球和5个白球,故共有球10个,所以从中任意摸出一个球,则P(摸到红球)=,故选C. 小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
 20.0米.
【解析】试题分析:此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
试题解析:如图:过点D作DG⊥AB,分别交AB、EF于点G、H,∵AB∥CD,DG⊥AB,AB⊥AC,∴四边形ACDG是矩形,∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,∵EF∥AB,∴,由题意,知FH=EF﹣...
20.0米.
【解析】试题分析:此题属于实际应用问题,解题的关键是将实际问题转化为数学问题进行解答;解题时要注意构造相似三角形,利用相似三角形的性质解题.
试题解析:如图:过点D作DG⊥AB,分别交AB、EF于点G、H,∵AB∥CD,DG⊥AB,AB⊥AC,∴四边形ACDG是矩形,∴EH=AG=CD=1.2,DH=CE=0.8,DG=CA=30,∵EF∥AB,∴,由题意,知FH=EF﹣... 如图,小山岗的斜坡AC的坡角α=45°,在与山脚C距离200米的D处,测得山顶A的仰角为26.6°,小山岗的高AB约为( ).(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)
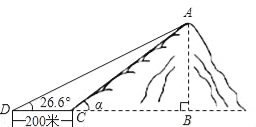
A.164m B.178m C.200m D.1618m
 C.
【解析】
试题分析:首先在Rt△ABC中,根据坡角的正切值用AB表示出BC,然后在Rt△DBA中,用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.∵在Rt△ABC中,=tanα=1,∴BC=AB,∵在RtADB中,∴=tan26.6°=0.50,即:BD=2AB,∵BD﹣BC=CD=200,∴2AB﹣AB=200,解得:AB=200米.
故选:C.
C.
【解析】
试题分析:首先在Rt△ABC中,根据坡角的正切值用AB表示出BC,然后在Rt△DBA中,用BA表示出BD,根据BD与BC之间的关系列出方程求解即可.∵在Rt△ABC中,=tanα=1,∴BC=AB,∵在RtADB中,∴=tan26.6°=0.50,即:BD=2AB,∵BD﹣BC=CD=200,∴2AB﹣AB=200,解得:AB=200米.
故选:C. 在△ABC中,∠A=105°,∠B=45°,cosC的值是( )
A.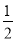 B.
B.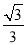 C.
C.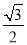 D.
D.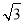
 C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C.
C
【解析】
试题分析:由三角形的内角和,得∠C=180°﹣∠A﹣∠B=30°,可得cosC=cos30°=,
故选:C. 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
 37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm.
37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm. 如下图所示,判断各组中的两个图形是否是全等图形.
A. 
B. 
C. 
D. 
 A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A.
A
【解析】全等图形需要大小相等,形状相同,原图中只有A同时符合这两个条件,B、C、D都只是形状相同,但大小不相等,
故选A. 
