15.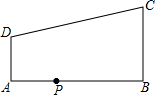 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
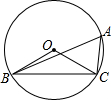
14. 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )| A. | ①②④ | B. | ①③ | C. | ①④ | D. | ①③④ |
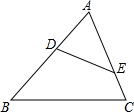
13. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
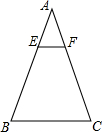
12. 如图,添加下列一个条件,不能使△ADE∽△ACB的是( )
如图,添加下列一个条件,不能使△ADE∽△ACB的是( )
 如图,添加下列一个条件,不能使△ADE∽△ACB的是( )
如图,添加下列一个条件,不能使△ADE∽△ACB的是( )| A. | DE∥BC | B. | ∠AED=∠B | C. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | D. | ∠ADE=∠C |
11. 如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )
如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )
 如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )
如图,在△ABC中,E、F分别是AB、AC上的点,EF∥BC,且$\frac{AE}{EB}$=$\frac{1}{2}$,若△AEF的面积为2,则四边形EBCF的面积为( )| A. | 4 | B. | 6 | C. | 16 | D. | 18 |
10.已知$\frac{a}{2}$=$\frac{b}{5}$,则$\frac{b-a}{a}$的值为( )
0 311159 311167 311173 311177 311183 311185 311189 311195 311197 311203 311209 311213 311215 311219 311225 311227 311233 311237 311239 311243 311245 311249 311251 311253 311254 311255 311257 311258 311259 311261 311263 311267 311269 311273 311275 311279 311285 311287 311293 311297 311299 311303 311309 311315 311317 311323 311327 311329 311335 311339 311345 311353 366461
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
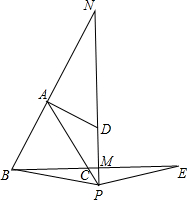 已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.
已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.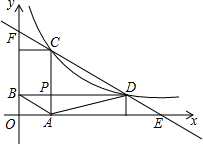 如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.
如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.