题目内容
14. 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )| A. | ①②④ | B. | ①③ | C. | ①④ | D. | ①③④ |
分析 由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ADB=∠AEB=90°,又由AB=AC,即可判定BD=CD,又由∠BAC=50°,可求得∠ABE的度数,继而判定AE≠CE,然后由三线合一的性质,判定∠BAD=∠CAE,即可求得劣弧DE的度数.
解答  解:∵AB是⊙O的直径,
解:∵AB是⊙O的直径,
∴∠ADB=∠AEB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD,故①正确;
∵∠BAC=50°,
∴∠ABC=∠C=65°,
∵∠ABE=90°-∠BAC=40°,故③正确;
∴∠CBE=∠ABC-∠ABE=25°,
∴AE≠CE,故②错误;
连接OE,
∵∠BOE=2∠BAC=100°,
∴$\widehat{BE}$的度数为100°,
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∴$\widehat{BD}$=$\widehat{DE}$,
∴劣弧DE的度数为50°,故④错误.
故选B.
点评 此题考查了圆周角定理、直角三角形的性质以及等腰三角形的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
4.已知一直角三角形的木板,三边的平方和为1800cm2,则斜边长为( )
| A. | 30cm | B. | 80cm | C. | 90cm | D. | 120cm |
5.20筐葡萄,以每筐20千克为标准,超过或不足的千克数分别用正、负数来表示,与标准质量的差值记录如下:
(1)20筐葡萄中,最重的一筐比最轻的一筐重5.5千克.
(2)与标准重量比较,20筐葡萄总计超过或不足多少千克?
(3)若葡萄每千克售价8元,则出售这20筐葡萄可卖多少元?
| 单位(千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 5 | 2 | 2 | 4 | 6 |
(2)与标准重量比较,20筐葡萄总计超过或不足多少千克?
(3)若葡萄每千克售价8元,则出售这20筐葡萄可卖多少元?
6.下列合并同类项正确的有( )
| A. | 2a+4a=8a2 | B. | 3x+2y=5xy | C. | 7x2-3x2=4 | D. | 9a2b-9ba2=0 |
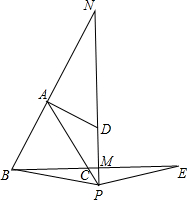 已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.
已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N. 如图,已知点D是△ABC的边AC上的一点,连接BD.∠ABD=∠C,AB=6,AD=4.
如图,已知点D是△ABC的边AC上的一点,连接BD.∠ABD=∠C,AB=6,AD=4.