题目内容
15.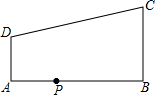 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.
解答 解:∵AB⊥BC,
∴∠B=90°.
∵AD∥BC
∴∠A=180°-∠B=90°,
∴∠PAD=∠PBC=90°.
设AP的长为x,则BP长为12-x.
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则AP:BP=AD:BC,
即x:(12-x)=4:9,
解得:x=$\frac{48}{13}$;
②若△APD∽△BCP,则AP:BC=AD:BP,
即x:9=4:(12-x),
解得:x=6.
∴满足条件的点P的个数是2个,
故选:B.
点评 本题主要考查了相似三角形的判定及性质,难度适中,进行分类讨论是解题的关键.

练习册系列答案
相关题目
10.已知$\frac{a}{2}$=$\frac{b}{5}$,则$\frac{b-a}{a}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
7.如果|a+2|+(b-1)2=0,那么代数式(a+b)2015的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2015 |
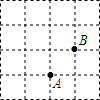 如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( )
如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有( ) 观察下面由“☆”组成的图案和算式,解答问题:
观察下面由“☆”组成的图案和算式,解答问题: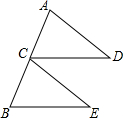 如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.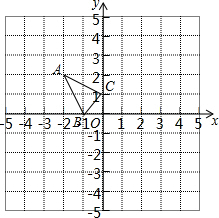 已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度). 已知⊙0的半径为R.求它的内接正三角形ABC的边长、边心距和面积.
已知⊙0的半径为R.求它的内接正三角形ABC的边长、边心距和面积.