题目内容
8.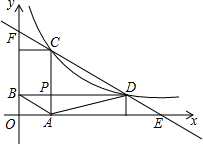 如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.
如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.(1)若点D的坐标为(6,1).
①求k的值;
②若△ACD的面积为6,求直线CD的解析式.
(2)若点C的横坐标为m,点D的纵坐标为n,直线CD与x轴相交于点E,与y轴相交于点F,探索m、n满足什么关系时,FC=CD=DE,请写出m、n的关系式并说明理由.
分析 (1)①把D坐标代入反比例解析式求出k的值即可;
②设C的坐标为(x,$\frac{6}{x}$),表示出OA与AC的长,由OM-OA求出AM的长,即为DP的长,以AC为底,DP为高表示出三角形ACD面积,将已知面积代入求出x的值,确定出C坐标,再由D的坐标,利用待定系数法求出直线CD解析式即可;
(2)根据C横坐标表示出纵坐标,即为AC的长,由FC=CD=DE,得到FC:FD=CN:BD=1:2,即可确定出m与n的关系式.
解答 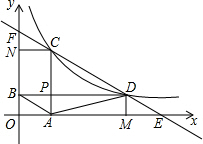 解:(1)①把D(6,1)代入y=$\frac{k}{x}$中,得:1=$\frac{k}{6}$,
解:(1)①把D(6,1)代入y=$\frac{k}{x}$中,得:1=$\frac{k}{6}$,
解得:k=6;
②设C坐标为(x,$\frac{6}{x}$),即OA=x,AC=$\frac{6}{x}$,
∵△ACD的面积为6,
∴$\frac{1}{2}$AC•DP=6,即$\frac{1}{2}$×$\frac{6}{x}$×(6-x)=6,
整理得:6-x=2x,
解得:x=2,即C(2,3),
设直线CD解析式为y=kx+b,
把C(2,3),D(6,1)代入得:$\left\{\begin{array}{l}{2k+b=3}\\{6k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$,
则直线CD解析式为y=-$\frac{1}{2}$x+4;
(2)把x=m代入y=$\frac{k}{x}$得:y=$\frac{k}{m}$;把y=n代入y=$\frac{k}{x}$得:x=$\frac{k}{n}$,
∴OA=m,AC=$\frac{k}{m}$,BD=$\frac{k}{n}$,DM=n,
∵FC=CD=DE,
∴FC:FD=CN:BD=1:2,
∴m:$\frac{k}{n}$=1:2,即mn=$\frac{k}{2}$,
则m、n满足mn=$\frac{k}{2}$时,FC=CD=DE.
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法求反比例函数解析式及一次函数解析式,三角形的面积,以及比例的性质,熟练掌握待定系数法是解本题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | ①③④⑥ | B. | ①③⑤ | C. | ①③④⑤ | D. | ③⑤⑥ |
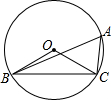 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
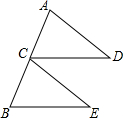 如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.
如图,已知点C为线段AB的中点,CD=BE,CD∥BE,请判断线段AD与CE的数量关系与位置关系,并说明理由.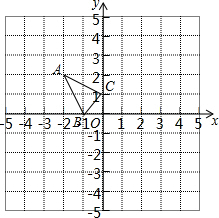 已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).
已知,△ABC在直角坐标平面内,三个顶点的坐标分别为A(-2,2)、B(-1,0)、C(0,1)(正方形网格中每个小正方形的边长是一个单位长度).