题目内容
13.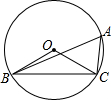 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
分析 由OB=OC,根据等边对等角的性质,可求得∠OBC的度数,继而求得∠BOC的度数,然后由在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得答案.
解答 解:∵OB=OC,
∴∠OBC=∠OCB=40°,
∴∠BOC=180°-∠OBC-∠OCB=100°,
∴∠A=$\frac{1}{2}$∠BOC=50°.
故选B.
点评 此题考查了圆周角定理以及等腰三角形的性质.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
3.等腰三角形两边分别为5和10,那么它的周长为( )
| A. | 20 | B. | 25 | C. | 15 | D. | 20或25 |
3.下列说法不正确的( )
| A. | 变量x,y满足x+3y=1,则y可以是x的函数 | |
| B. | 变量x,y满足y=x,则y是x的函数 | |
| C. | 变量x,y满足y2=x2,则y是x的函数 | |
| D. | 变量x,y满足y=x2,则y是x的函数 |
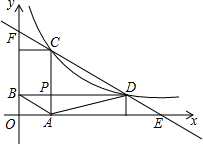 如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD.
如图,已知点C、D是反比例函数y=$\frac{k}{x}$(x>0)的图象上的两个动点,点C在点D的上方,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A、B,CA与DB相交于点P,连接AB、AD. 如图,在△ABC中,∠B=∠ACB=$\frac{1}{4}$∠BAC,CD是AB边上的高,CD=5,求BC的长.
如图,在△ABC中,∠B=∠ACB=$\frac{1}{4}$∠BAC,CD是AB边上的高,CD=5,求BC的长.