题目内容
9.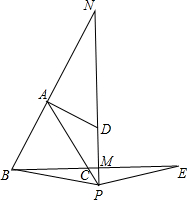 已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.
已知:如图,△ABC是等边三角形,点P、E分别是AC、BC的延长线上的点,且AP=CE,点M是BE的中点,PM和BA的延长线相交于点N.(1)试说明△NAP是等腰三角形;
(2)过点A作AD⊥AB,交PN于点D,试证明ND=2DP.
分析 (1)作PN∥AB交BE于N,先证得△PCN是等边三角形,进而证得CM=NM,然后根据三线合一的性质证得∠CPM=∠NPM=30°,PN⊥BE,根据三角形外角的性质得出∠PAN=120°,然后根据三角形内角和定理得出∠N=30°,从而证得△NAP是等腰三角形;
(2)根据已知求得∠DAP=∠APN=30°,得出AD=PD,然后根据含30°的直角三角形的性质得出ND=2AD,即可证得ND=2DP.
解答  证明:(1)作PN∥AB交BE于N,
证明:(1)作PN∥AB交BE于N,
∴∠PNC=∠ABC=60°,
∵∠PCN=∠ACB=60°,
∴△PCN是等边三角形,
∴CN=PC,
∵AP=CE,
∴AP-CP=CE-CN,
即AC=EN,
∵BC=AC,
∴BC=EN,
∵BM=EM,
∴CM=NM,
∴∠CPM=∠NPM=30°,PN⊥BE,
∵∠PAN=120°,
∴∠N=30°,
∴∠APN=∠N,
∴PA=AN,
∴△NAP是等腰三角形;
(2)∵AD⊥AB,∠BAC=60°,
∴∠DAP=30°,
∴∠DAP=∠APN=30°,
∴AD=PD,
在RT△DAN中,∠N=30°,
∴ND=2AD,
∴ND=2PD.
点评 本题考查了等边三角形的判定和性质,等腰三角形的判定和性质,含30°的直角三角形的性质,平行线的性质,三角形外角的性质,作出辅助线构建等边三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.有一个数值转换器,程序如图所示,当输入的数x为81时,输出的数y的值是( )


| A. | 9 | B. | 3 | C. | $\sqrt{3}$ | D. | ±$\sqrt{3}$ |
14. 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
 如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )
如图,AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,且∠BAC=50°,给出下列四个结论:①BD=CD,②AE=CE,③∠ABE=40°,④劣弧DE的度数为25°.其中正确结论的序号是( )| A. | ①②④ | B. | ①③ | C. | ①④ | D. | ①③④ |
18.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如下.
(1)根据题意,填写下列表格;
(2)A、B两点能否相遇?如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;
(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.
(1)根据题意,填写下列表格;
| 时间(s) | 0 | 5 | 7 | x |
| A点位置 | 19 | -1 | -9 | -4x+19 |
| B点位置 | -8 | 17 | 27 | 5x-8 |
(3)A、B两点能否相距18个单位长度?如果能,求相距18个单位长度的时刻;如不能,请说明理由.
 如图,一条公路的转弯处是一段圆弧AB.
如图,一条公路的转弯处是一段圆弧AB.