6.若方程组$\left\{\begin{array}{l}{2x+y=5}\\{x+2y=a-3}\end{array}\right.$的解满足x+y的值为非负数,则a满足( )
| A. | a<-2 | B. | a≤-2 | C. | a≤2 | D. | a≥-2 |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
3.在等腰直角三角形ABC中,斜边AB=2$\sqrt{2}$cm,则三角形ABC的面积等于( )
| A. | 2cm2 | B. | 4cm2 | C. | $\sqrt{2}$cm2 | D. | 2$\sqrt{2}$cm2 |
2.若a+b+c=0,那么关于x的方程ax2+bx+c=0(a≠0)必有一根是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
20.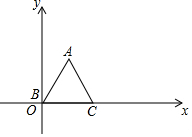 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )| A. | (4033,$\sqrt{3}$) | B. | (4033,0) | C. | (4036,$\sqrt{3}$) | D. | (4036,0) |
19.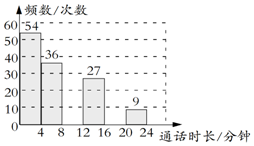 手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
(1)a的值为3;补全频数分布直方图;
(2)样本中通话时长在20<x≤24之间的9个数据分别为21分08秒,22分25秒,22分14秒,21分23秒,23分48秒,21分02秒,23分16秒,23分42秒,21分17秒,求这9个通话时长的平均数;
(3)请估计小乔家这800个通话中通话时长超过12分钟的次数.
0 298400 298408 298414 298418 298424 298426 298430 298436 298438 298444 298450 298454 298456 298460 298466 298468 298474 298478 298480 298484 298486 298490 298492 298494 298495 298496 298498 298499 298500 298502 298504 298508 298510 298514 298516 298520 298526 298528 298534 298538 298540 298544 298550 298556 298558 298564 298568 298570 298576 298580 298586 298594 366461
 手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.
手机在现如今的社会几乎是每人一部,在近期的一项研究结果显示,普通用户平均每天查看手机大约110次,其中大约22次是打电话.小乔想了解家人打电话的通话时长(即每次的通话时间)的分布情况,于是他收集了他家800个通话时长的数据,这些数据均不超过24分钟,他从中随机选取了若干个数据作为样本,统计结果如下表,并将结果绘制成如图所示的频数分布直方图.| 通话时长x/分钟 | 次数 |
| 0<x≤4 | 54 |
| 4<x≤8 | 36 |
| 8<x≤12 | 4a |
| 12<x≤16 | 27 |
| 16<x≤20 | 4a |
| 20<x≤24 | 3a |
(2)样本中通话时长在20<x≤24之间的9个数据分别为21分08秒,22分25秒,22分14秒,21分23秒,23分48秒,21分02秒,23分16秒,23分42秒,21分17秒,求这9个通话时长的平均数;
(3)请估计小乔家这800个通话中通话时长超过12分钟的次数.
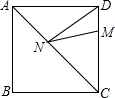 如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20.
如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20. 如图,在△ABC中,过点B作EB⊥AB,交AC于点E,BE平分∠CBD,90°+∠C=∠BDC,则∠A的度数为45°.
如图,在△ABC中,过点B作EB⊥AB,交AC于点E,BE平分∠CBD,90°+∠C=∠BDC,则∠A的度数为45°.