题目内容
20.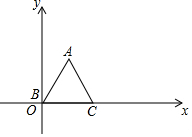 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )| A. | (4033,$\sqrt{3}$) | B. | (4033,0) | C. | (4036,$\sqrt{3}$) | D. | (4036,0) |
分析 利用已知点坐标得出等边△ABC边长为2,根据三角函数可得等边△ABC的高,顶点A的坐标分别为(4,0),(5,$\sqrt{3}$),(8,0),(9,$\sqrt{3}$),…,进而得出点的坐标变化规律,即可得出答案.
解答 解:顶点A的坐标分别为(4,0),(5,$\sqrt{3}$),(8,0),(9,$\sqrt{3}$),
…,
2017÷2=1008…1,
1008×4+4=4036,
故顶点A的坐标是(4036,0).
故选:D.
点评 此题主要考查了坐标与图形的变化,正确得出点的坐标变化规律是解题关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.若m2+m-1=0,则m3+2m2+2017的值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
12.下列事件是随机事件的是( )
| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 有一名运动员奔跑的速度是80米/秒 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
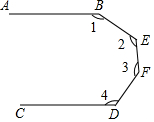 如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.
如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°. 如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,则∠DAC+∠C=90°.
如图,在等腰三角形ABC中,AB=AC,AD平分∠BAC,则∠DAC+∠C=90°.