题目内容
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
分析 已知AB,BO根据勾股定理即可求得AO的值,根据对角线长即可计算菱形ABCD的面积.
解答 解:
∵四边形ABCD是菱形,AC=12,
∴AO=$\frac{1}{2}$AC=6,
∵菱形对角线互相垂直,
∴△ABO为直角三角形,
∴BO=$\sqrt{A{B}^{2}-O{A}^{2}}$=8,
BD=2BO=16,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×12×16=96.
故选C.
点评 本题考查了菱形对角线互相垂直平分的性质,菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求AO的值是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
15.下列各数化简后与|3|相等的是( )
| A. | 3-1 | B. | (-1)3 | C. | |-3| | D. | -(-$\frac{1}{3}$) |
13.已知直线y=x+$\frac{3}{2}$与直线y=kx-1相交于点P,若点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集为( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
20.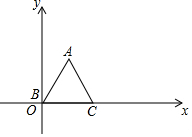 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )| A. | (4033,$\sqrt{3}$) | B. | (4033,0) | C. | (4036,$\sqrt{3}$) | D. | (4036,0) |
17.下列分式是最简分式的是( )
| A. | $\frac{15bc}{12a}$ | B. | $\frac{{3{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{a^2}-{b^2}}}{2(a+b)}$ | D. | $\frac{{{a^2}+{b^2}}}{a+b}$ |
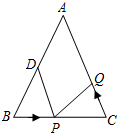 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.