14.直线y=2x经过( )
| A. | 第二、四象限 | B. | 第一、二象限 | C. | 第三、四象限 | D. | 第一、三象限 |
13.下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(环) | 8.9 | 9.1 | 8.9 | 9.1 |
| 方差 | 3.3 | 3.8 | 3.8 | 3.3 |
| A. | 丁 | B. | 丙 | C. | 乙 | D. | 甲 |
12.点A(x1,y1)和B(x2,y2)在y=$\frac{4}{x}$的图象上,若x1>x2,则( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法比较 |
11.下列计算结果中,正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{(-4)(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$=6 | C. | $\sqrt{12}$$-\sqrt{3}$=$\sqrt{3}$ | D. | $\sqrt{(-7)^{2}}$=±7 |
8.关于x的一元二次方程x2-6x+k=0有两个不相等的实数根,则实数k的取值范围是( )
| A. | k≤9 | B. | k<9 | C. | k≥9 | D. | k>9 |
7.在一个不透明的袋子中,有3个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出1个球,摸到白球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
6.方程(x-3)(x+1)=0的解是( )
0 297429 297437 297443 297447 297453 297455 297459 297465 297467 297473 297479 297483 297485 297489 297495 297497 297503 297507 297509 297513 297515 297519 297521 297523 297524 297525 297527 297528 297529 297531 297533 297537 297539 297543 297545 297549 297555 297557 297563 297567 297569 297573 297579 297585 297587 297593 297597 297599 297605 297609 297615 297623 366461
| A. | x=0 | B. | x=3 | C. | x=3或x=-1 | D. | x=0或x=3 |
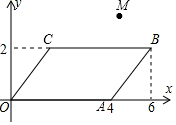 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.
如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.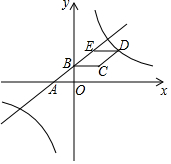 如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.