题目内容
9.计算:(1)$\sqrt{1\frac{3}{5}}$×2$\sqrt{3}$×(-$\frac{1}{2}$$\sqrt{10}$);
(2)$\sqrt{3}$($\frac{1}{3}$+$\sqrt{2\frac{2}{3}}$);
(3)$\frac{m}{3}$•$\sqrt{\frac{3n}{m}}$•$\frac{2}{n}$$\sqrt{\frac{3{m}^{2}}{n}}$;
(4)$\frac{2}{y}$$\sqrt{x{y}^{5}}$×(-$\frac{3}{2}$$\sqrt{{x}^{3}y}$)×$\sqrt{\frac{x}{{y}^{5}}}$.
分析 (1)根据二次根式的乘法法则运算;
(2)根据二次根式的乘法法则运算;
(3)根据二次根式的乘法法则运算;
(4)根据二次根式的乘法法则运算.
解答 解:(1)原式=-2×$\frac{1}{2}$×$\sqrt{\frac{8}{5}×3×10}$
=-4$\sqrt{3}$;
(2)原式=$\frac{\sqrt{3}}{3}$+$\sqrt{3×\frac{8}{3}}$
=$\frac{\sqrt{3}}{3}$+2$\sqrt{2}$;
(3)原式=$\frac{m}{3}$•$\frac{2}{n}$•$\sqrt{\frac{3n}{m}•\frac{3{m}^{2}}{n}}$
=$\frac{2m\sqrt{m}}{n}$;
(4)原式=-$\frac{2}{y}$•$\frac{3}{2}$•$\sqrt{x{y}^{5}•{x}^{3}y•\frac{x}{{y}^{5}}}$
=-$\frac{{x}^{2}\sqrt{y}}{y}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
19.某球形流感病毒的直径约为0.000 000 085m,用科学记数法表示该数据为( )
| A. | 8.5-8 | B. | 85×10-9 | C. | 0.85×10-7 | D. | 8.5×10-8 |
20.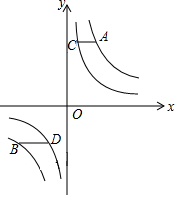 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
 如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )
如图,点A、B在反比例函数y=$\frac{m}{x}$的图象上,点C、D在反比例函数y=$\frac{n}{x}$的图象上,m>n>0,AC∥BD∥x轴,AC、BD在x轴的两侧,AC=$\frac{4}{5}$,BD=$\frac{4}{3}$,AC与BD间的距离为$\frac{24}{5}$,则m-n的值是( )| A. | $\frac{3}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{5}$ | D. | $\frac{12}{5}$ |
17.如图,下列各图象反映的是两个变量之间的关系,其中表示匀速运动的是( )


| A. | (3)(4) | B. | (2)(3) | C. | (1)(2) | D. | (2)(4) |
4.抛物线y=-3(x+1)2+3的顶点坐标是( )
| A. | (-1,3) | B. | (1,3) | C. | (-1,-3) | D. | (0,3) |
14.直线y=2x经过( )
| A. | 第二、四象限 | B. | 第一、二象限 | C. | 第三、四象限 | D. | 第一、三象限 |
1.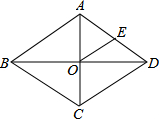 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
 如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )
如图,在菱形ABCD中,对角线AC、BD交于点O,E为AD的中点,菱形ABCD的周长为28,则OE的长等于( )| A. | 3.5 | B. | 4 | C. | 7 | D. | 14 |
18.在数学竞赛的选拔活动中,对甲、乙两名同学的成绩经过统计分析可得:$\overline{{x}_{甲}}$=94(分),$\overline{{x}_{乙}}$=94(分);S${\;}_{甲}^{2}$=1.02,S${\;}_{乙}^{2}$=0.85,下列结论正确的是( )
| A. | 甲的成绩比乙的成绩好 | B. | 甲的成绩比乙的成绩稳定 | ||
| C. | 应该选择乙同学参加竞赛 | D. | 不能衡量两名同学的成绩优劣 |
19.下列根式中,最简二次根式是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{24}$ | C. | $\sqrt{30}$ | D. | $\sqrt{36}$ |