4.我县万德隆商场有A、B两种商品的进价和售价如表:
已知:用2400元购进A种商品的数量与用3000元购进B种商品的数量相同.
(1)求m的值;
(2)该商场计划同时购进的A、B两种商品共200件,其中购进A种商品x件,实际进货时,生产厂家对A种商品的出厂价下调a(50<a<70)元出售,若商场保持同种商品的售价不变,商场售完这200件商品的总利润为y元.
①求y关于x的函数关系式;
②若限定A种商品最多购进120件最少购进100件,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
| 商品 价格 | A | B |
| 进价(元/件) | m | m+20 |
| 售价(元/件) | 160 | 240 |
(1)求m的值;
(2)该商场计划同时购进的A、B两种商品共200件,其中购进A种商品x件,实际进货时,生产厂家对A种商品的出厂价下调a(50<a<70)元出售,若商场保持同种商品的售价不变,商场售完这200件商品的总利润为y元.
①求y关于x的函数关系式;
②若限定A种商品最多购进120件最少购进100件,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
2.在解方程组$\left\{\begin{array}{l}{3x+2y=2①}\\{2x+2y=-1②}\end{array}\right.$中,①-②所得的方程是( )
| A. | x=1 | B. | 5x=-1 | C. | x=3 | D. | 5x=3 |
1.下列方程中,解是x=2的是( )
| A. | 3x+1=2x-1 | B. | 3x-1=2x+1 | C. | 3x+2x-2=0 | D. | 3x+2x+2=0 |
16.用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C的含量及购买这两种原料的价格如下表所示:
(1)现配制这种饮料10kg,要求至少含有4200单位的维生素C,写出所需甲种原料的质量x(kg)应满足的不等式.
(2)如果仅要求购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量x(kg)的取值范围.
0 284373 284381 284387 284391 284397 284399 284403 284409 284411 284417 284423 284427 284429 284433 284439 284441 284447 284451 284453 284457 284459 284463 284465 284467 284468 284469 284471 284472 284473 284475 284477 284481 284483 284487 284489 284493 284499 284501 284507 284511 284513 284517 284523 284529 284531 284537 284541 284543 284549 284553 284559 284567 366461
| 原料 | 甲 | 乙 |
| 维生素C的含量∕(单位∕kg) | 600 | 100 |
| 原料价格∕(元∕kg) | 8 | 4 |
(2)如果仅要求购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量x(kg)的取值范围.
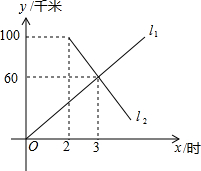 如图,A、B两地相距100千米,甲骑电动车,乙骑摩托车分别从A、B两地出发,相向而行,假设它们都保持匀速行驶,l1表示甲到A地的距离y/千米和骑车时间x/时之间的函数关系;l2表示乙到A地的距离y/千米和骑车时间x/时之间的函数关系.
如图,A、B两地相距100千米,甲骑电动车,乙骑摩托车分别从A、B两地出发,相向而行,假设它们都保持匀速行驶,l1表示甲到A地的距离y/千米和骑车时间x/时之间的函数关系;l2表示乙到A地的距离y/千米和骑车时间x/时之间的函数关系.