12.以下列各组数据为边长,可以构成等腰三角形的是( )
| A. | 2,3,4 | B. | 5,5,10 | C. | 2,2,1 | D. | 1,2,3 |
10.已知三角形的周长小于13,各边长均为整数且三边各不相等,那么这样的三角形个数共有( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.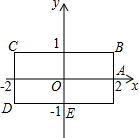 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙由点(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是( )| A. | (-1,-1) | B. | (2,0) | C. | (-1,1) | D. | (1,-1) |
6.阅读与计算:阅读以下材料,并完成相应的任务.
任务:请根据以上材料,通过计算求出裴波那契数列中的第1个数和第2个数.
0 282639 282647 282653 282657 282663 282665 282669 282675 282677 282683 282689 282693 282695 282699 282705 282707 282713 282717 282719 282723 282725 282729 282731 282733 282734 282735 282737 282738 282739 282741 282743 282747 282749 282753 282755 282759 282765 282767 282773 282777 282779 282783 282789 282795 282797 282803 282807 282809 282815 282819 282825 282833 366461
斐波那契(约1170-1250)是意大利数学家,他研究了一列数, 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一 这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到 的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的 瓣数恰是斐波那契数列中的数,斐波那契数列还有很多有趣的性质, 在实际生活中也有广泛的应用. 斐波那契数列中的第n个数可以用$\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^{n}-(\frac{1-\sqrt{5}}{2})^{n}]$ 表示(其中n≥1),这是用无理数表示有理数的一个范例. |
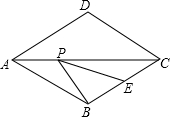 如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为2$\sqrt{3}$+2.
如图,菱形ABCD的边长为4,∠DAB=60°,E为BC的中点,在对角线AC上存在一点P,使△PBE的周长最小,则△PBE的周长的最小值为2$\sqrt{3}$+2.