14.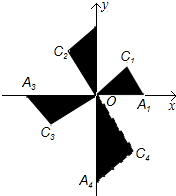 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
 在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )
在平面直角坐标系xOy中,Rt△OA1C1、Rt△OA2C2、Rt△OA3C3、Rt△OA4C4…斜边都在坐标轴上,∠A1OC1=∠A2OC2=∠A3OC3…=30°,若点A1的坐标(3,0),OA1=OC2,OA2=OC3,OA3=OC4…则依此规律OA2016的长为( )| A. | 3×($\frac{3}{2}$$\sqrt{3}$)2013 | B. | 3×($\frac{3}{2}\sqrt{3}$)2014 | C. | 3×($\frac{3\sqrt{3}}{2}$)2015 | D. | 3×($\frac{3\sqrt{3}}{2}$)2016 |
13.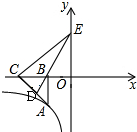 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
12.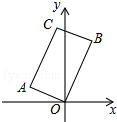 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
 如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{1}{2}$,4) | B. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | C. | ($\frac{3}{2}$,3)、(-$\frac{1}{2}$,4) | D. | ($\frac{7}{4}$,$\frac{7}{2}$)、(-$\frac{2}{3}$,4) |
11.若分式方程$\frac{x-a}{x+1}$=a无解,则a的值( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
10.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
下列结论不正确的是( )
| 居民户数 | 1 | 3 | 2 | 4 |
| 月用电量(度/户) | 40 | 50 | 55 | 60 |
| A. | 众数是60 | B. | 平均数是54 | C. | 中位数是55 | D. | 方差是29 |
9.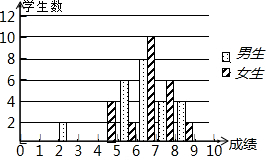 为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
(1)请补充完成下面的成绩统计分析表:
(2)男生说他们的合格率、优秀率均高于女生,所以他们的成绩好于女生,但女生不同意男生的说法,认为女生的成绩要好于男生,请给出两条支持女生观点的理由;
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?
0 281782 281790 281796 281800 281806 281808 281812 281818 281820 281826 281832 281836 281838 281842 281848 281850 281856 281860 281862 281866 281868 281872 281874 281876 281877 281878 281880 281881 281882 281884 281886 281890 281892 281896 281898 281902 281908 281910 281916 281920 281922 281926 281932 281938 281940 281946 281950 281952 281958 281962 281968 281976 366461
 为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下(1)请补充完成下面的成绩统计分析表:
| 平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
| 男生 | 6.9 | 2.4 | 7 | 91.7% | 16.7% |
| 女生 | 7 | 1.3 | 7 | 83.3% | 8.3% |
(3)体育老师说,咱班的合格率基本达标,但优秀率太低,我们必须加强体育锻炼,两周后的目标是:全班优秀率达到50%.如果女生新增优秀人数恰好是男生新增优秀人数的两倍,那么男、女生分别新增多少优秀人数才能达到老师的目标?