题目内容
13.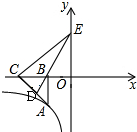 如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )
如图,已知点A在反比例函数y=$\frac{k}{x}$(x<0)上,作Rt△ABC,点D是斜边AC的中点,连DB并延长交y轴于点E,若△BCE的面积为8,则k的值为( )| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
分析 根据反比例函数系数k的几何意义,证明△ABC∽△EOB,根据相似比求出BA•BO的值,从而求出△AOB的面积.
解答 解:∵△BCE的面积为8,
∴$\frac{1}{2}$BC•OE=8,
∴BC•OE=16,
∵点D为斜边AC的中点,
∴BD=DC,
∴∠DBC=∠DCB=∠EBO,
又∠EOB=∠ABC,
∴△EOB∽△ABC,
∴$\frac{BC}{OB}=\frac{AB}{OE}$,
∴AB•OB•=BC•OE
∴k=AB•BO=BC•OE=16,
故选:C.
点评 本题考查了反比例函数系数k的几何意义,解决本题的关键是证明△EOB∽△ABC,得到AB•OB•=BC•OE.

练习册系列答案
相关题目
1.下列各数中,没有平方根的是( )
| A. | (-2)2 | B. | 64 | C. | $\frac{1}{2}$ | D. | -22 |
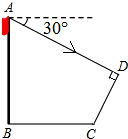 小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长
小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆AB影子恰好落在水平地面BC和斜坡面CD上,测得旗杆在水平地面上的影长BC=20m,在斜坡坡面上的影长