题目内容
16.(1)解方程:(2x-1)2=x(3x+2)-7(2)先化简再求值($\frac{a-2}{{a}^{2}+2a}$-$\frac{a-1}{{a}^{2}+4a+4}$)÷$\frac{a-4}{a+2}$,其中a=$\sqrt{2}$-1.
分析 (1)先把方程整理为一元二次方程的一般形式,再用因式分解法求出x的值即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可.
解答 解:(1)原方程可化为x2-6x+8=0,即(x-2)(x-4)=0,
解得x1=2,x2=4;
(2)原式=[$\frac{a-2}{a(a+2)}$-$\frac{a-1}{(a+2)^{2}}$]•$\frac{a+2}{a-4}$
=$\frac{(a+2)(a-2)-a(a-1)}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{a-4}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{1}{a(a+2)}$,
当a=$\sqrt{2}$-1时,原式=$\frac{1}{(\sqrt{2}-1)(\sqrt{2}+1)}$=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
4.下列命题中逆命题是真命题的是( )
| A. | 对顶角相等 | |
| B. | 若两个角都是45°,那么这两个角相等 | |
| C. | 全等三角形的对应角相等 | |
| D. | 两直线平行,同位角相等 |
11.若分式方程$\frac{x-a}{x+1}$=a无解,则a的值( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0 |
1.在下列APP图标的设计图案中,可以看做中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.我们是这样研究一个数绝对值的性质的:当a>0时,如a=6,则|a|=|6|=6,此时a的绝对值是它本身;当a=0时,|a|=0,此时a的绝对值是零;当a<0时,如a=-6,则|a|=|-6|=6,此时a的绝对值是它的相反数.这种分析问题的方法所体现的数学思想是( )
| A. | 转化思想 | B. | 分类思想 | C. | 数形结合思想 | D. | 公理化思想 |
5.下列根式中,与$\sqrt{20}$互为同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
6.方程x-2=0的解是( )
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | 2 | D. | -2 |
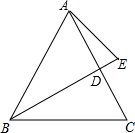 在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.
在△ABC中,点E在角平分线BD的延长线上,且∠EAC=∠ABE,若2∠BAC+∠E=180°,tan∠EAC=$\frac{1}{2}$,AE=5,则BE的长是11.