3.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
2.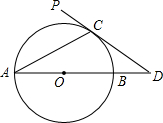 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )| A. | 2$\sqrt{2}$-2 | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
1.已知矩形的周长为36m,矩形绕着它的一条边旋转形成一个圆柱,设矩形的一条边长为xm,圆柱的侧面积为ym2,则y与x的函数关系式为( )
| A. | y=-2πx2+18πx | B. | y=2πx2-18πx | C. | y=-2πx2+36πx | D. | y=2πx2-36πx |
20.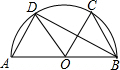 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
19. 在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
 在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )
在如图所示的花坛的图案中,圆形的内部有菊花组成的内接等边三角形,则这个图案( )| A. | 是轴对称图形但不是中心对称图形 | |
| B. | 既是轴对称图形又是中心对称图形 | |
| C. | 是中心对称图形但不是轴对称图形 | |
| D. | 既不是轴对称图形又不是中心对称图形 |
18.二次函数y=x2+x的图象与y轴的交点坐标是( )
0 281223 281231 281237 281241 281247 281249 281253 281259 281261 281267 281273 281277 281279 281283 281289 281291 281297 281301 281303 281307 281309 281313 281315 281317 281318 281319 281321 281322 281323 281325 281327 281331 281333 281337 281339 281343 281349 281351 281357 281361 281363 281367 281373 281379 281381 281387 281391 281393 281399 281403 281409 281417 366461
| A. | (0,1) | B. | (0,-1) | C. | (0,0) | D. | (-1,0) |
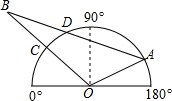 如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.
如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.