题目内容
7.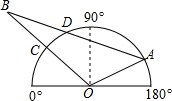 如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.
如图,半圆O是一个量角器,△AOB为一纸片,点A在半圆上,边AB与半圆相交于点D,边OB与半圆相交于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠B等于20度.
分析 连结OD,如图,根据题意得∠DOC=25°,∠AOD=90°,由于OD=OA,则∠ADO=45°,然后利用三角形外角性质得∠ADO=∠B+∠DOB,得出∠B=45°-25°=20°即可.
解答 解:连结OD,如图
则∠DOC=70°-45°=25°,∠AOD=160°-70°=90°,
∵OD=OA,
∴∠ADO=45°,
∵∠ADO=∠B+∠DOB,
∴∠B=45°-25°=20°.
故答案为:20.
点评 本题考查了圆周角定理、等腰三角形的性质、三角形的外角性质;由等腰三角形的性质得出∠ADO=45°是解决问题的突破口.

练习册系列答案
相关题目
17.$\sqrt{4}$的平方根等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
15.下列事件是必然事件的是( )
| A. | 2016年两路镇房价一定下降 | |
| B. | 两个负数相乘,结果是正数 | |
| C. | 渝北区明天一定会下雪 | |
| D. | 小明努力学习,这次数学考试一定得满分 |
2.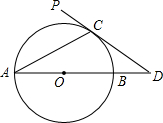 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
 如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )
如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC,若∠D=2∠CAD,CD=2,则BD的长为( )| A. | 2$\sqrt{2}$-2 | B. | 2-$\sqrt{2}$ | C. | 2$\sqrt{2}$-1 | D. | $\sqrt{2}$-1 |
12.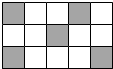 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
 一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )
一只小狗在如图的方砖上走来走去,最终停在白色方砖上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
16.已知3x>-6y,则下列不等式不一定成立的是( )
| A. | $\frac{1}{2}$x>-y | B. | x+2>2-2y | C. | -x<2y | D. | $\frac{1}{x}>-\frac{1}{2y}$ |
17.在军事演习中,利用雷达跟踪某一“敌方”目标,需要确定该目标的( )
| A. | 方向 | B. | 距离 | C. | 大小 | D. | 方向与距离 |
 如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.
如图,AB∥CD,∠CDE=121°,GF交∠DEB的平分线EF于点F,∠AGF=140°,求∠F的度数.