题目内容
5.小强掷两枚质地均匀的骰子,每个骰子的六个面上分别刻有1到6的点数,则两枚骰子点数相同的概率为$\frac{1}{6}$.分析 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两枚骰子点数相同的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
| (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
所以两枚骰子点数相同的概率=$\frac{6}{36}$=$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 本题考查了列表法与树状图法求随机事件的概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.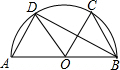 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
 如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )
如图,$\widehat{AB}$是半圆,连接AB,点O为AB的中点,点C、D在$\widehat{AB}$上,连接AD、CO、BC、BD、OD.若∠COD=62°,且AD∥OC,则∠ABD的大小是( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
17.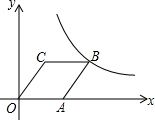 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
14.已知等边△ABC的一边长为10,则它的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
15.十八世纪瑞士数学家欧拉证明了简单多面体的顶点数(V)、面树(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
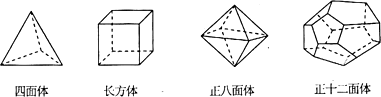
(1)根据上面多面体模型,填写表格中的空格:
(2)根据上面的表格,猜想顶点数(V)、面数(F)、棱数(E)之间存在的关系式是V+F-E=2(用所给的字母表达);
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.

(1)根据上面多面体模型,填写表格中的空格:
| 多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
| 四面体 | 4 | 4 | 6 |
| 长方体 | 8 | 6 | 12 |
| 正八面体 | 6 | 8 | 12 |
| 正十二面体 | 20 | 12 | 30 |
(2)若一个多面体的面数比顶点数少14,且有48条棱,则这个多面体的面数是18;
(3)有一个玻璃饰品的外形是简单多面体,它共有24个顶点,每个顶点处都有3条棱,设该多面体的面数为x,求x的值.
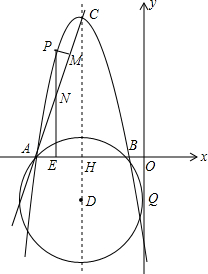 在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H
在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H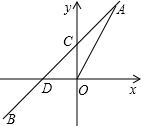 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.