题目内容
3.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
分析 先根据所给的数据求出抛物线的解析式,再进行判断即可.
解答 解:∵抛物线过点(-2,0)和(0,6),则$\left\{\begin{array}{l}{-4-2b+c=0}\\{c=6}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=1}\\{c=6}\end{array}\right.$,
∴抛物线的解析式为y=-x2+x+6,
∴抛物线与y轴的交点为(0,6),故①正确;
抛物线的对称是:直线x=-$\frac{b}{2a}$=$\frac{1}{2}$,故②错误;
抛物线与x轴的两个交点为(-2,0),(3,0),它们之间的距离是5,故③错误;
抛物线开口向下,则在对称轴左侧,y随x的增大而增大,故④正确.
正确答案为①④.
故选:D.
点评 本题考查了用待定系数法求二次函数的解析式、二次函数的性质以及抛物线与x轴的交点问题,掌握待定系数法求得函数解析式是解决问题的关键.

练习册系列答案
相关题目
18.二次函数y=x2+x的图象与y轴的交点坐标是( )
| A. | (0,1) | B. | (0,-1) | C. | (0,0) | D. | (-1,0) |
15.一个扇形的弧长为5π,面积是15π,则该扇形的圆心角是( )
| A. | 120° | B. | 150° | C. | 210° | D. | 240° |
12.用棋子摆出下列一组图形:
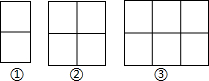
(1)填写表格:
(2)如果某一图形共有99枚棋子,你知道它是第几个图形吗?

(1)填写表格:
| 图形编号 | 1 | 2 | 3 | 4 | … | n |
| 图形中的棋子 | 6 | 9 | 12 | 15 | … | 3n+3 |
 如图是半径为2的圆.
如图是半径为2的圆.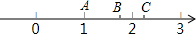 如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.
如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.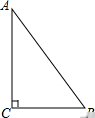 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.