题目内容
18.二次函数y=x2+x的图象与y轴的交点坐标是( )| A. | (0,1) | B. | (0,-1) | C. | (0,0) | D. | (-1,0) |
分析 令x=0,求出y的值,然后写出与y轴的交点坐标即可.
解答 解:当x=0时,y=0,
则二次函数二次函数y=x2+x的图象与y轴的交点坐标是(0,0),
故选:C.
点评 本题考查了二次函数图象上点的坐标特征,熟练掌握函数与坐标轴的交点的求解方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )
 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1+∠4=180° | D. | ∠4=∠5 |
6.在圆周长计算公式C=2πr中,对半径不同的圆,变量有( )
| A. | C,r | B. | C,π,r | C. | C,πr | D. | C,2π,r |
3.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
7.现在宁波市的出租车的起步价为10元(行驶不超过3.5千米),以后每增加1千米,加价2元,每趟另加2元燃油附加费.现在某人乘出租车行驶s千米的路程(s>3.5)所需的费用是( )
| A. | 12+2s | B. | 10+2(s+1) | C. | 12+2s-3.5 | D. | 12+2(s-3.5) |
8.解方程$\frac{x+1}{2}$-$\frac{x-3}{6}$=1时,下列去分母正确的是( )
| A. | 3x+1-x-3=1 | B. | 3(x+1)-(x-3)=1 | C. | 3(x+1)-x-3=6 | D. | 3(x+1)-(x-3)=6 |
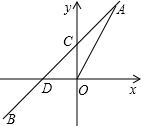 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象交于点A(m,2),与y轴的交点为C,与x轴的交点为D.