11.若$\frac{x}{y}$=$\frac{4}{5}$,则$\frac{2x-y}{x+y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{3}{2}$ |
9.有这样一个问题:探究函数y=$\frac{1}{x-1}$+x的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
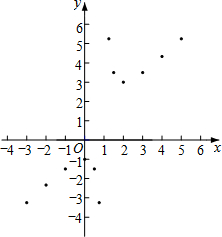
0 279044 279052 279058 279062 279068 279070 279074 279080 279082 279088 279094 279098 279100 279104 279110 279112 279118 279122 279124 279128 279130 279134 279136 279138 279139 279140 279142 279143 279144 279146 279148 279152 279154 279158 279160 279164 279170 279172 279178 279182 279184 279188 279194 279200 279202 279208 279212 279214 279220 279224 279230 279238 366461
小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{3}{4}$ | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{13}{4}$ | -$\frac{7}{3}$ | -$\frac{3}{2}$ | -1 | -$\frac{3}{2}$ | -$\frac{13}{4}$ | $\frac{21}{4}$ | $\frac{7}{2}$ | 3 | $\frac{7}{2}$ | m | $\frac{21}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
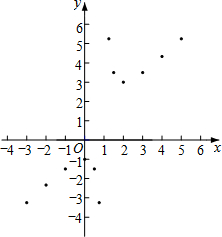
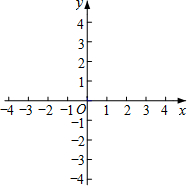 在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D.
在平面直角坐标系xOy中,抛物线y=x2+bx+c经过点A(-1,t),B(3,t),与y轴交于点C(0,-1).一次函数y=x+n的图象经过抛物线的顶点D. 北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)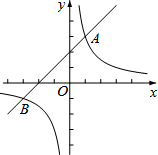 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,且点A的坐标为(1,m).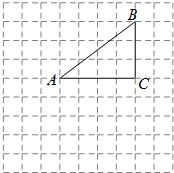 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1. 如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,交⊙O于点C,CD=2,求弦AB的长.
如图,⊙O的半径为5,AB为弦,OC⊥AB,交AB于点D,交⊙O于点C,CD=2,求弦AB的长.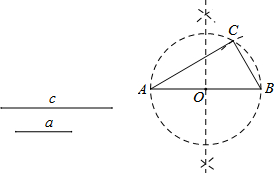 阅读下面材料:
阅读下面材料: