题目内容
9.有这样一个问题:探究函数y=$\frac{1}{x-1}$+x的图象与性质.小东根据学习函数的经验,对函数y=$\frac{1}{x-1}$+x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{x-1}$+x的自变量x的取值范围是x≠1;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | 0 | $\frac{1}{2}$ | $\frac{3}{4}$ | $\frac{5}{4}$ | $\frac{3}{2}$ | 2 | 3 | 4 | 5 | … |
| y | … | -$\frac{13}{4}$ | -$\frac{7}{3}$ | -$\frac{3}{2}$ | -1 | -$\frac{3}{2}$ | -$\frac{13}{4}$ | $\frac{21}{4}$ | $\frac{7}{2}$ | 3 | $\frac{7}{2}$ | m | $\frac{21}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(2,3),结合函数的图象,写出该函数的其它性质(一条即可):该函数没有最大值,也没有最小值.
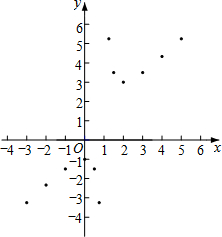
分析 (1)由图表可知x≠0;
(2)根据图表可知当x=4时的函数值为m,把x=4代入解析式即可求得;
(3)根据坐标系中的点,用平滑的直线连接即可;
(4)观察图象即可得出该函数的其他性质.
解答 解:(1)x≠1,
故答案为x≠1;
(2)令x=4,
∴y=$\frac{1}{4-1}$+4=$\frac{13}{3}$;
∴m=$\frac{13}{3}$;
(3)如图
(4)该函数的其它性质:
该函数没有最大值,也没有最小值;
故答案为该函数没有最大值,也没有最小值.
点评 本题考查了反比例函数的图象和性质,根据图表画出函数的图象是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
20.在Rt△ABC中,∠C=90°,BC=1,那么AB的长为( )
| A. | sinA | B. | cosA | C. | $\frac{1}{cosA}$ | D. | $\frac{1}{sinA}$ |
17. 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5,则cosB的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
14.某圆锥的母线长为6cm,其底面圆半径为3cm,则它的侧面积为( )
| A. | 18πcm2 | B. | 18cm2 | C. | 36πcm2 | D. | 36cm2 |
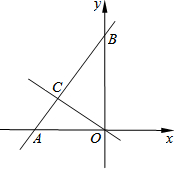 如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.
如图,一次函数y=mx+2m+3的图象与y=-$\frac{1}{2}$x的图象交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.