如图.在边长为1的小正方形组成的网格中.△ABC的三个顶点均在格点上．将△ABC绕点A顺时针旋转90°得到△AB1C1．(1)在网格中画出△AB1C1,(2)计算点B旋转到B1的过程中所经过的路径长．题目和参考答案——青夏教育精英家教网—

题目内容

6．

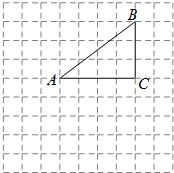如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上．将△ABC绕点A顺时针旋转90°得到△AB₁C₁．
（1）在网格中画出△AB₁C₁；
（2）计算点B旋转到B₁的过程中所经过的路径长．（结果保留π）

分析（1）利用网格特点和旋转的性质画出点B、C的对应点B₁、C₁即可得到△AB₁C₁；
（2）点B旋转到B₁的过程中所经过的路径为以A为圆心，AB为半径，圆心角为90°的弧，于是根据弧长公式可计算出点B旋转到B₁的过程中所经过的路径长．

解答解：（1）如图，△AB₁C₁为所作；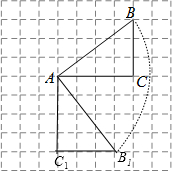

（2）AB=$\sqrt{{3}^{2}+{4}^{2}}$=5，
所以B旋转到B₁的过程中所经过的路径长=$\frac{90•π•5}{180}$=$\frac{5}{2}$π．

点评本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了弧长公式．

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

17．阅读下面材料：
如图1，在平面直角坐标系xOy中，直线y₁=ax+b与双曲线y₂=$\frac{k}{x}$交于A（1，3）和B（-3，-1）两点．
观察图象可知：
①当x=-3或1时，y₁=y₂；
②当-3＜x＜0或x＞1时，y₁＞y₂，即通过观察函数的图象，可以得到不等式ax+b＞$\frac{k}{x}$的解集．
有这样一个问题：求不等式x³+4x²-x-4＞0的解集．
某同学根据学习以上知识的经验，对求不等式x³+4x²-x-4＞0的解集进行了探究．

下面是他的探究过程，请将（2）、（3）、（4）补充完整：
（1）将不等式按条件进行转化：
当x=0时，原不等式不成立；
当x＞0时，原不等式可以转化为x²+4x-1＞$\frac{4}{x}$；
当x＜0时，原不等式可以转化为x²+4x-1＜$\frac{4}{x}$；
（2）构造函数，画出图象
设y₃=x²+4x-1，y₄=$\frac{4}{x}$，在同一坐标系中分别画出这两个函数的图象．
双曲线y₄=$\frac{4}{x}$如图2所示，请在此坐标系中画出抛物线y₃=x²+4x-1；（不用列表）
（3）确定两个函数图象公共点的横坐标
观察所画两个函数的图象，猜想并通过代入函数解析式验证可知：满足y₃=y₄的所有x的值为±1和-4；
（4）借助图象，写出解集
结合（1）的讨论结果，观察两个函数的图象可知：不等式x³+4x²-x-4＞0的解集为x＞1或-4＜x＜-1．

14．若△ABC∽△DEF，相似比为1：3，则△ABC与△DEF的面积比为（　　）

1．某农科院在相同条件下做了某种玉米种子发芽率的试验，结果如下：

种子总数	100	400	800	1000	3500	7000	9000	14000
发芽种子数	91	354	716	901	3164	5613	8094	12614
发芽的频率	0.91	0.885	0.895	0.901	0.904	0.902	0.899	0.901

则该玉米种子发芽的概率估计值为0.9（结果精确到0.1）．

11．若$\frac{x}{y}$=$\frac{4}{5}$，则$\frac{2x-y}{x+y}$的值为（　　）

18．

如图，AB为⊙O的弦，AB=8，OA=5，OP⊥AB于P，则OP=3．

15．

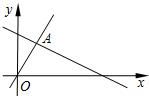如图，函数y=2x和y=ax+4的图象相交于点A（1，m），则不等式2x＜ax+4的解集为x＜1．

16．2°=120′?=7200″；
1800″=30′?=0.5°．

试题分类