题目内容
3．
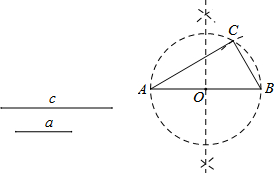阅读下面材料：在数学课上，老师提出如下问题：
尺规作图：作Rt△ABC，使其斜边AB=c，一条直角边BC=a．
已知线段a，c如图．
小芸的作法如下：
①取AB=c，作AB的垂直平分线交AB于点O；
②以点O为圆心，OB长为半径画圆；
③以点B为圆心，a长为半径画弧，与⊙O交于点C；
④连接BC，AC．
则Rt△ABC即为所求．
老师说：“小芸的作法正确．”
请回答：小芸的作法中判断∠ACB是直角的依据是直径所对的圆周角为直角．
分析 根据圆周角定理的推论求解．
解答 解：小芸的作法中判断∠ACB是直角的依据是直径所对的圆周角为直角．
故答案为直径所对的圆周角为直角．
点评 本题考查了作图-复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了圆周角定理．
练习册系列答案
相关题目
18．
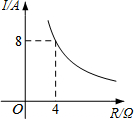已知一块蓄电池的电压为定值，以此蓄电池为电源时，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）
已知一块蓄电池的电压为定值，以此蓄电池为电源时，电流I（A）与电阻R（Ω）之间的函数关系如图，则电流I关于电阻R的函数解析式为（ ）| A． | $I=\frac{4}{R}$ | B． | $I=\frac{8}{R}$ | C． | $I=\frac{32}{R}$ | D． | $I=-\frac{32}{R}$ |
北京联合张家口成功申办2022年冬奥会后，滑雪运动已成为人们喜爱的娱乐健身项目．如图是某滑雪场为初学者练习用的斜坡示意图，出于安全因素考虑，决定将斜坡的倾角由45°降为30°，已知原斜坡坡面AB长为200米，点D，B，C在同一水平地面上，求改善后的斜坡坡角向前推进的距离BD．（结果保留整数．参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{6}$≈2.45）
15．已知：⊙O是△ABC的外接圆，∠OAB=40°，则∠ACB的大小为（ ）
| A． | 20° | B． | 50° | C． | 20°或160° | D． | 50°或130° |
12．设2+$\sqrt{3}$的整数部分用a表示，小数部分用b表示，4-$\sqrt{3}$的整数部分用c表示，小数部分用d表示，则$\frac{b+d}{ac}$的值为（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{6}$ | C． | $\frac{5}{6}$ | D． | $\frac{1}{3}$（$\sqrt{3}$-1） |