题目内容
8. 北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由45°降为30°,已知原斜坡坡面AB长为200米,点D,B,C在同一水平地面上,求改善后的斜坡坡角向前推进的距离BD.(结果保留整数.参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
分析 根据题意和正切的概念分别求出CB、CD的长,计算即可.
解答 解:∵∠C=90°,∠ABC=45°,
∴AC=BC=100$\sqrt{2}$≈141米,
tan∠D=$\frac{AC}{CD}$,
∴CD=$\frac{AC}{tan30°}$=100$\sqrt{6}$≈245米,
∴BD=CD-CB=104米,
答:改善后的斜坡坡角向前推进的距离BD为104米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
19.把10cm长的线段进行黄金分割,则较长线段的长($\sqrt{5}$≈2.236,精确到0.01)是( )
| A. | 3.09cm | B. | 3.82cm | C. | 6.18cm | D. | 7.00cm |
16. 如图,AB是⊙O的直径,C,D是圆上两点,∠AOC=50°,则∠D等于( )
如图,AB是⊙O的直径,C,D是圆上两点,∠AOC=50°,则∠D等于( )
 如图,AB是⊙O的直径,C,D是圆上两点,∠AOC=50°,则∠D等于( )
如图,AB是⊙O的直径,C,D是圆上两点,∠AOC=50°,则∠D等于( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
13.已知:在Rt△ABC中,∠C=90°,sinA=$\frac{3}{4}$,则cosB的值为( )
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
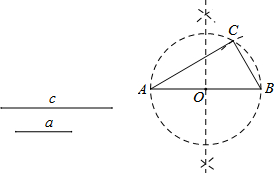 阅读下面材料:
阅读下面材料: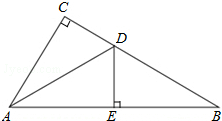 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.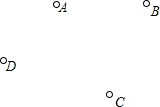 已知平面上有四个点,按要求画图:
已知平面上有四个点,按要求画图: