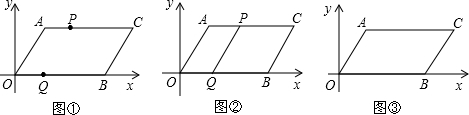
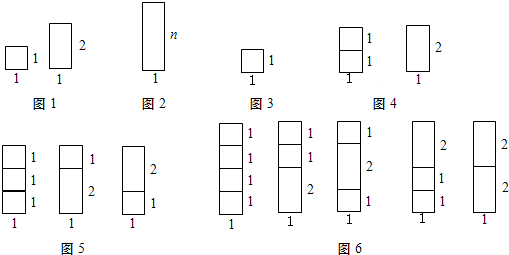
0 257594 257602 257608 257612 257618 257620 257624 257630 257632 257638 257644 257648 257650 257654 257660 257662 257668 257672 257674 257678 257680 257684 257686 257688 257689 257690 257692 257693 257694 257696 257698 257702 257704 257708 257710 257714 257720 257722 257728 257732 257734 257738 257744 257750 257752 257758 257762 257764 257770 257774 257780 257788 366461

 如图,在△ABC中,∠C=90°,D是AC边上一点,且AD=BD=5,tan∠CBD=
如图,在△ABC中,∠C=90°,D是AC边上一点,且AD=BD=5,tan∠CBD= 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
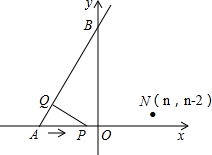 如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3
如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3