题目内容
 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)试说明:AE∥CF;
(2)BC平分∠DBE吗?为什么?
考点:平行线的判定与性质
专题:
分析:(1)根据邻补角和已知求出∠BDC=∠1,根据平行线的判定推出即可;
(2)求出∠FDA=∠C,推出AD∥CB,求出∠ADB=∠CBD,∠ADB=∠CBD,推出∠CBD=∠CBE即可.
(2)求出∠FDA=∠C,推出AD∥CB,求出∠ADB=∠CBD,∠ADB=∠CBD,推出∠CBD=∠CBE即可.
解答:解:(1)∵∠1+∠2=180°,∠2+∠CDB=180°,
∴∠BDC=∠1,
∴AE∥CF;
(2)BC平分∠DBE,
理由是:∵DA平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,
∴∠A=∠FDA,∠FDB=∠EBD,
∵∠A=∠C,
∴∠FDA=∠C,
∴AD∥CB,
∴∠ADB=∠CBD,∠ADB=∠CBD,
∴∠CBD=∠CBE,
即BC平分∠DBE.
∴∠BDC=∠1,
∴AE∥CF;
(2)BC平分∠DBE,
理由是:∵DA平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,
∴∠A=∠FDA,∠FDB=∠EBD,
∵∠A=∠C,
∴∠FDA=∠C,
∴AD∥CB,
∴∠ADB=∠CBD,∠ADB=∠CBD,
∴∠CBD=∠CBE,
即BC平分∠DBE.
点评:本题考查了平行线的性质和判定的应用,注意:①两直线平行,内错角相等,②两直线平行,同位角相等.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,函数y=kx的图象与y=
如图,函数y=kx的图象与y=| 5-k |
| x |
A、
| ||||
B、3
| ||||
C、3
| ||||
D、
|
已知a-b>0,则下列不等式一定成立的是( )
| A、a-2>b-2 | ||||
| B、-2a>-2b | ||||
| C、a2>b2 | ||||
D、
|

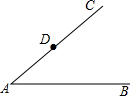 如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)
如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)