题目内容
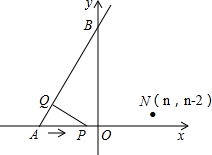 如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3
如图,已知射线AB与x轴和y轴分别交于点A(-3,0)和点B(0,3| 3 |
(1)当n=3时,若PQ恰好经过点N,求t的值;
(2)连接BP,记△BPQ面积为S△BPQ,△ABP面积为S△ABP.
①当S△BPQ≤
| 1 |
| 2 |
②当S△BPQ=
| 1 |
| 3 |
考点:一次函数综合题
专题:
分析:(1)构造如下草图分析,由点A(-3,0)和点B(0,3
),得出,∠BAO=60°,得出在Rt△PNH中,∠NPH=30°,NH=1,PH=
,进一步利用OH=xN=3,OA=3,求得答案即可;
(2)分两种情况:①当S△BPQ=
S△ABP,②当S△BPQ=
S△ABP时;在分别按点Q在点B下方时,当点Q在点B上方时,探讨得出答案即可.
| 3 |
| 3 |
(2)分两种情况:①当S△BPQ=
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:(1)如图

由点A(-3,0)和点B(0,3
),
在Rt△PNH中,∠BAO=60°.
当n=3时,点N(3,1).
在Rt△PNH中,∠NPH=30°,NH=1,PH=
,
又OH=xN=3,OA=3,
∴AP=6+
.
即t=6+
.
(2)①当S△BPQ=
S△ABP时,由于两个三角形同高,即有BQ=
AB,
需要考虑两种可能:
当点Q在点B下方时,点Q为线段AB的中点,此时容易出求AP=2AQ=6,即t=6,
当点Q在点B上方时,AQ=9,此时容易出求AP=2AQ=18,即t=18,
相应的,当S△BPQ≤
S△ABP时,求t的取值范围是6≤t≤18.
②当S△BPQ=
S△ABP时,由(2)①中的方法可求出BQ=2,相应点Q有两个可能的坐标是(-1,2
)、(1,4
).
由代数式(a-n)2+(b-n+2)2的特点,本质上求点Q到点N的最小距离,而点N(n,n-2)在直线y=x-2,也就是点Q到直线y=x-2的距离就是QN的最小值.
(Ⅰ)当点Q(-1,2
)时,作QN⊥直线y=x-2于点N,此时N(
,
),
根据待定系数法求出直线QN的解析式为y=-x+2
-1.
(Ⅱ)当点Q(1,4
)时,作QN⊥直线y=x-2于点N,此时N(
,
),
根据待定系数法求出直线QN的解析式为y=-x+4
+1.
综上,直线QN的解析式为y=-x+2
-1或y=-x+4
+1.

由点A(-3,0)和点B(0,3
| 3 |
在Rt△PNH中,∠BAO=60°.
当n=3时,点N(3,1).
在Rt△PNH中,∠NPH=30°,NH=1,PH=
| 3 |
又OH=xN=3,OA=3,
∴AP=6+
| 3 |
即t=6+
| 3 |
(2)①当S△BPQ=
| 1 |
| 2 |
| 1 |
| 2 |
需要考虑两种可能:
当点Q在点B下方时,点Q为线段AB的中点,此时容易出求AP=2AQ=6,即t=6,
当点Q在点B上方时,AQ=9,此时容易出求AP=2AQ=18,即t=18,
相应的,当S△BPQ≤
| 1 |
| 2 |
②当S△BPQ=
| 1 |
| 3 |
| 3 |
| 3 |
由代数式(a-n)2+(b-n+2)2的特点,本质上求点Q到点N的最小距离,而点N(n,n-2)在直线y=x-2,也就是点Q到直线y=x-2的距离就是QN的最小值.
(Ⅰ)当点Q(-1,2
| 3 |
2
| ||
| 2 |
2
| ||
| 2 |
根据待定系数法求出直线QN的解析式为y=-x+2
| 3 |
(Ⅱ)当点Q(1,4
| 3 |
4
| ||
| 2 |
4
| ||
| 2 |
根据待定系数法求出直线QN的解析式为y=-x+4
| 3 |
综上,直线QN的解析式为y=-x+2
| 3 |
| 3 |
点评:此题考查一次函数的综合运用,分别将两种可能的坐标代入代数式整得出关于n的二次函数,利用二次函数的最值分析求出点Q的坐标实现问题求解.

练习册系列答案
相关题目
在下列四个图形中,△DEF能由△ABC经过平移得到的图形是( )
A、 |
B、 |
C、 |
D、 |
已知点P(2-4m,m-2)在第二象限,则m的取值范围是( )
A、m>
| ||
| B、m<2 | ||
| C、m>2 | ||
D、
|
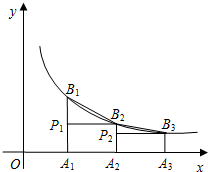 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y= 如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.
如图,在直角三角形中,两直角边长为a,b斜边上的高为h,判断以ab,ah,bh为边长的三角形形状并说明理由.
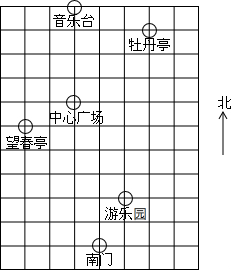 春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)
春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)