 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
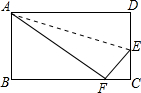 折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |
 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |