题目内容
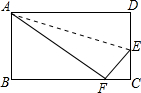 折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )A、5
| ||
B、5
| ||
| C、12cm | ||
| D、13cm |
考点:翻折变换(折叠问题)
专题:
分析:首先根据勾股定理求出BF的长度,进而求出CF的长度;再根据勾股定理求出EF的长度问题即可解决.
解答: 解:由题意得:
解:由题意得:
AF=AD,EF=DE(设为x),
∵四边形ABCD为矩形,
∴AF=AD=BC=10,DC=AB=8;∠ABF=90°;
由勾股定理得:
BF2=102-82=36,
∴BF=6,CF=10-6=4;
在直角三角形EFC中,
由勾股定理得:
x2=42+(8-x)2,
解得:x=5,
∴AE2=102+52=125,
∴AE=5
(cm).
故选A.
 解:由题意得:
解:由题意得:AF=AD,EF=DE(设为x),
∵四边形ABCD为矩形,
∴AF=AD=BC=10,DC=AB=8;∠ABF=90°;
由勾股定理得:
BF2=102-82=36,
∴BF=6,CF=10-6=4;
在直角三角形EFC中,
由勾股定理得:
x2=42+(8-x)2,
解得:x=5,
∴AE2=102+52=125,
∴AE=5
| 5 |
故选A.
点评:该命题以矩形为载体,以图形的翻折为方法,以考查翻折变换的性质及其应用为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
若x2-y2=3,则(x+y)2(x-y)2的值是( )
| A、3 | B、6 | C、9 | D、18 |
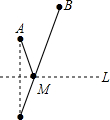
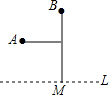
 已知一次函数y=-2x+3
已知一次函数y=-2x+3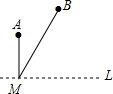
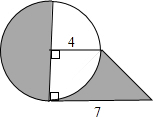 求阴影部分的面积:
求阴影部分的面积: 如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为
如图,BC是⊙O的直径,A是圆上一点,AD⊥BC,垂足为点D.P为