题目内容
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |
考点:翻折变换(折叠问题)
专题:
分析:首先求出AB的长度,根据翻折变换的性质及勾股定理求出BE的长度问题即可解决.
解答: 解:由勾股定理得:
解:由勾股定理得:
AB2=62+82=100,
∴AB=10;
由题意得:BE=AE(设为x),
则CE=8-x;
由勾股定理得:
x2=62+(8-x)2,
解得:x=
;
∴DE2=(
)2-52=
×
,
∴DE=3.75;
故选C.
 解:由勾股定理得:
解:由勾股定理得:AB2=62+82=100,
∴AB=10;
由题意得:BE=AE(设为x),
则CE=8-x;
由勾股定理得:
x2=62+(8-x)2,
解得:x=
| 25 |
| 4 |
∴DE2=(
| 25 |
| 4 |
| 45 |
| 4 |
| 5 |
| 4 |
∴DE=3.75;
故选C.
点评:该命题主要考查了翻折变换及其应用问题;解题的关键是根据翻折变换的性质找出图中相等的边或角;灵活运用有关定理来解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
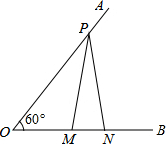 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=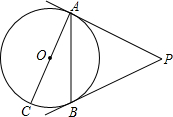 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC=6,∠P=50°,求:
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC=6,∠P=50°,求:
 已知CD是Rt△ABC斜边上的高线,且AB=10,若sin∠ACD=
已知CD是Rt△ABC斜边上的高线,且AB=10,若sin∠ACD=
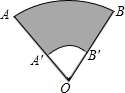 如图所示是两个同心圆被其两条半径所截得到的图形,已知
如图所示是两个同心圆被其两条半径所截得到的图形,已知 如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.
如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.