题目内容
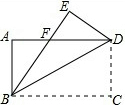 如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3
如图,把一张矩形的纸片沿对角线折叠,若BE平分∠ABD,FE=3,CD=3| 3 |
考点:翻折变换(折叠问题)
专题:
分析:首先根据勾股定理求出DF的长度,然后借助面积公式即可解决问题.
解答: 解:如图,根据题意得:
解:如图,根据题意得:
DE=DC=3
,∠E=∠C=90°;
由勾股定理得:
DF2=DE2+EF2=(3
)2+32=36,
∴DF=6,
∴S△BFD=
DF•AB=
×6×3
=9
,
即△BFD的面积S=9
,
故答案为:9
.
 解:如图,根据题意得:
解:如图,根据题意得:DE=DC=3
| 3 |
由勾股定理得:
DF2=DE2+EF2=(3
| 3 |
∴DF=6,
∴S△BFD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
即△BFD的面积S=9
| 3 |
故答案为:9
| 3 |
点评:该命题主要考查了翻折变换及其应用问题;同时还考查了勾股定理、矩形的性质、三角形的面积公式等几何知识点.

练习册系列答案
相关题目
 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
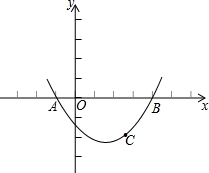 如图,已知抛物线过点A(-1,0),B(4,0),C(
如图,已知抛物线过点A(-1,0),B(4,0),C( 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,如果AD=13,tan∠DCB=
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,如果AD=13,tan∠DCB=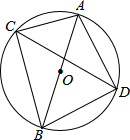 已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长.
已知A、B、C三点位于⊙O上,其中AB连线过圆心,DC是∠ACB的角平分线,D点也在⊙O上,已知AC=6,AB=10,求BC、AD、BD的长.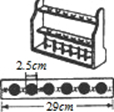 如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为
如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为