题目内容
几何模型:
条件:如图1,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图2,正方形是大家喜爱的一种轴对称图形,它的对角线所在的直线就是对称轴.现在有一个边长为2的正方形ABCD,E为AB的中点,P是AC上一动点. 请求出EP+PB的最小值.

(2)如图3,∠AOC=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
条件:如图1,A、B是直线l同旁的两个定点.
问题:在直线l上确定一点P,使PA+PB的值最小.
方法:作点A关于直线l的对称点A′,连结A′B交l于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图2,正方形是大家喜爱的一种轴对称图形,它的对角线所在的直线就是对称轴.现在有一个边长为2的正方形ABCD,E为AB的中点,P是AC上一动点. 请求出EP+PB的最小值.

(2)如图3,∠AOC=45°,P是∠AOB内一点,PO=10,Q、R分别是OA、OB上的动点,求△PQR周长的最小值.
考点:轴对称-最短路线问题
专题:
分析:(1)根据正方形的性质,点B、D关于AC对称,连接DE与AC的交点即为所求点P,EP+PB的最小值等于DE,然后利用勾股定理列式计算即可得解;
(2)作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2,求出△PQR周长的最小值=P1P2,连接OP1、OP2,根据轴对称的性质求出△OP1P2是等腰直角三角形,然后求解即可.
(2)作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2,求出△PQR周长的最小值=P1P2,连接OP1、OP2,根据轴对称的性质求出△OP1P2是等腰直角三角形,然后求解即可.
解答: 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,
∴点B、D关于AC对称,
∴连接DE与AC的交点即为所求点P,EP+PB的最小值=DE,
由勾股定理得,DE=
=
;
(2)作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2,
则△PQR周长的最小值=P1P2,
连接OP1、OP2,则OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,
所以,OP1=OP2,∠P1OP2=2∠AOB=2×45°=90°,
所以,△OP1P2是等腰直角三角形,
∵PO=10,
∴PO1=10,
∴P1P2=
PO1=10
,
即△PQR周长的最小值为10
.
 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,∴点B、D关于AC对称,
∴连接DE与AC的交点即为所求点P,EP+PB的最小值=DE,
由勾股定理得,DE=
| 22+12 |
| 5 |
(2)作点P关于OA的对称点P1,关于OB的对称点P2,连接P1P2,
则△PQR周长的最小值=P1P2,
连接OP1、OP2,则OP=OP1=OP2,∠AOP=∠AOP1,∠BOP=∠BOP2,
所以,OP1=OP2,∠P1OP2=2∠AOB=2×45°=90°,
所以,△OP1P2是等腰直角三角形,
∵PO=10,
∴PO1=10,
∴P1P2=
| 2 |
| 2 |
即△PQR周长的最小值为10
| 2 |
点评:本题考查了利用轴对称确定最短路线问题,等腰直角三角形的判定与性质,熟记轴对称的性质以及最短路线的确定方法是解题的关键.

练习册系列答案
相关题目
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |
 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2
已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
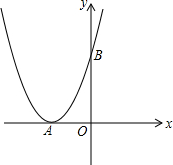 如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.
如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B. 求如图中几何体的体积.
求如图中几何体的体积. 如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是
如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是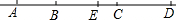 如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求:
如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求: