题目内容
如图，已知AD是△ABC的角平分线，求证：| AB |
| AC |
| BD |
| DC |
考点：平行线分线段成比例
专题：证明题
分析：过C点作CE∥AD交BA的延长线于E，如图，由于CE∥AD，根据平行线分线段成比例定理得到
=
，根据平行线的性质得到∠DAC=∠ACE，∠BAD=∠E，
再根据角平分线的定义得∠DAC=∠BAD，所以∠ACE=∠E，根据等腰三角形的判定得到AE=AC，则有
=
．
| AB |
| AE |
| BD |
| DC |
再根据角平分线的定义得∠DAC=∠BAD，所以∠ACE=∠E，根据等腰三角形的判定得到AE=AC，则有
| AB |
| AC |
| BD |
| DC |
解答：证明：过C点作CE∥AD交BA的延长线于E，如图，
∵CE∥AD，
∴
=
，∠DAC=∠ACE，∠BAD=∠E，
∵AD是△ABC的角平分线，
∴∠DAC=∠BAD，
∴∠ACE=∠E，
∴AE=AC，
∴
=
．
∵CE∥AD，
∴
| AB |
| AE |
| BD |
| DC |
∵AD是△ABC的角平分线，
∴∠DAC=∠BAD，
∴∠ACE=∠E，
∴AE=AC，
∴
| AB |
| AC |
| BD |
| DC |
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．
练习册系列答案
名校课堂系列答案
相关题目
求如图中几何体的体积．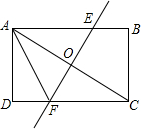
如图所示，将长方形ABCD沿直线EF对折，使顶点A与C重合在一起，折痕EF分别交CD、AB于点F，E交对角线AC相交于点O，已知AB=18cm，BC=12cm．
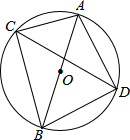已知：如图所示，AB=10cm，BC=8cm，CD平分∠ACB．