题目内容
 如图,在纸片△ABC中,AC=6,∠A=30°,∠C=90°,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为
如图,在纸片△ABC中,AC=6,∠A=30°,∠C=90°,将∠A沿DE折叠,使点A与点B重合,则折痕DE的长为考点:翻折变换(折叠问题)
专题:
分析:首先根据直角三角形的性质求出斜边AB的长度,进而求出AD的长度;再次利用直角三角形的边角关系即可求出DE的长度.
解答: 解:如图,由题意得:
解:如图,由题意得:
∠ADE=∠BDE=90°,AD=BD;
∵AC=6,∠A=30°,∠C=90°,
∴AB=2BC(设BC为x),
由勾股定理得:(2x)2=x2+62,
解得:x=2
,
∴AD=BD=2
,
∵tan30°=
,
∴DE=2,
故答案为2.
 解:如图,由题意得:
解:如图,由题意得:∠ADE=∠BDE=90°,AD=BD;
∵AC=6,∠A=30°,∠C=90°,
∴AB=2BC(设BC为x),
由勾股定理得:(2x)2=x2+62,
解得:x=2
| 3 |
∴AD=BD=2
| 3 |
∵tan30°=
| DE |
| AD |
∴DE=2,
故答案为2.
点评:该命题主要考查了翻折变换及其应用问题;同时还渗透了对直角三角形的边角关系等几何知识点的考查.

练习册系列答案
相关题目
有四包方便面,每包以标准克数(108克)为基数,超过的克数记作正数,不足的克数记作负数,以下数据中最接近标准克数的是( )
| A、+2 | B、-3 | C、+3 | D、+4 |
 如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由
如图,AB是⊙O的直径,弦CD⊥AB,∠ACD=30°,CD=6,则由 |
| AD |
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 如图:已知l1∥l2∥l3,CH=2cm,AG=1.5cm,BG=2.5cm,EF=5cm,求DH、EK的长.
如图:已知l1∥l2∥l3,CH=2cm,AG=1.5cm,BG=2.5cm,EF=5cm,求DH、EK的长.
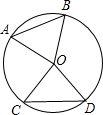 如图,在⊙O中,AB、CD是弦,根据条件填空.
如图,在⊙O中,AB、CD是弦,根据条件填空.