下列图形既是轴对称图形,又是中心对称图形的是( )
| A、等边三角形 | B、平行四边形 |
| C、正五边形 | D、正方形 |
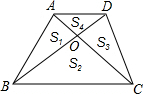 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )| A、S1=S3 |
| B、S2=2S4 |
| C、S2=2S1 |
| D、S1•S3=S2•S4 |
| A、等边三角形 | B、平行四边形 |
| C、正五边形 | D、正方形 |
 如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )
如图,已知在梯形ABCD中,AD∥BC,BC=2AD,如果对角线AC与BD相交于点O,△AOB、△BOC、△COD、△DOA的面积分别记作S1、S2、S3、S4,那么下列结论中,不正确的是( )| A、S1=S3 |
| B、S2=2S4 |
| C、S2=2S1 |
| D、S1•S3=S2•S4 |