题目内容
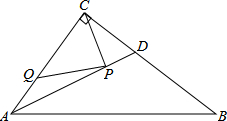如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）| A、2.4 | B、4 | C、4.8 | D、5 |
考点：轴对称-最短路线问题
专题：
分析：过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，由AD是∠BAC的平分线．得出PQ=PM，这时PC+PQ有最小值，即CM的长度，运用勾股定理求出AB，再运用S△ABC=
AB•CM=
AC•BC，得出CM的值，即PC+PQ的最小值．
| 1 |
| 2 |
| 1 |
| 2 |
解答：解：如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，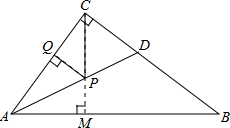
∵AD是∠BAC的平分线．
∴PQ=PM，这时PC+PQ有最小值，即CM的长度，
∵AC=6，BC=8，∠ACB=90°，
∴AB=
=
=10．
∵S△ABC=
AB•CM=
AC•BC，
∴CM=
=
=
，
即PC+PQ的最小值为
．
故选：C．
∵AD是∠BAC的平分线．
∴PQ=PM，这时PC+PQ有最小值，即CM的长度，
∵AC=6，BC=8，∠ACB=90°，
∴AB=
| AC2+BC2 |
| 62+82 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=
| AC•BC |
| AB |
| 6×8 |
| 10 |
| 24 |
| 5 |
即PC+PQ的最小值为
| 24 |
| 5 |
故选：C．
点评：本题主要考查了轴对称问题，解题的关键是找出满足PC+PQ有最小值时点P和Q的位置．
练习册系列答案
相关题目
一个扇形的圆心角为120°，半径为15cm，则它的弧长为（ ）
| A、5πcm | B、10πcm |
| C、15πcm | D、20πcm |
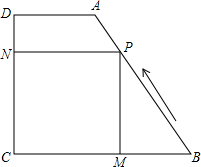如图，在梯形ABCD中，AD∥BC，DC⊥BC，AD=2，CD=4，tanB=
