题目内容
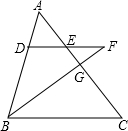已知如图，D是△ABC的边AB上一点，DE∥BC，交边AC于点E，延长DE至点F，使EF=DE，联结BF，交边AC于点G，联结CF（1）求证：
| AE |
| AC |
| EG |
| CG |
（2）如果CF2=FG•FB，求证：CG•CE=BC•DE．
考点：相似三角形的判定与性质
专题：证明题
分析：（1）首先证明△ADE∽△ABC，△EFG∽△CBG，根据相似三角形的对应边的比相等，以及DE=EF即可证得；
（2）首先证明△CFG∽△BFC，证得
=
，∠FCE=∠CBF，然后根据平行线的性质证明∠FEG=∠CEF，即可证得△EFG∽△ECF，则
=
=
，即可证得
=
，则所证结论即可得到．
（2）首先证明△CFG∽△BFC，证得
| CG |
| BC |
| FG |
| FC |
| EF |
| EC |
| FG |
| FC |
| DE |
| EC |
| CG |
| FG |
| DE |
| EC |
解答：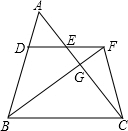
证明：（1）∵DE∥BC，
∴△ADE∽△ABC，△EFG∽△CBG，
∴
=
，
=
，
又∵DE=EF，
∴
=
，
∴
=
；
（2）∵CF2=FG•FB，
∴
=
，
又∵∠CFG=∠CFB，
∴△CFG∽△BFC，
∴
=
，∠FCE=∠CBF，
又∵DF∥BC，
∴∠EFG=∠CBF，
∴∠FCE=∠EFG，
又∵∠FEG=∠CEF，
∴△EFG∽△ECF，
∴
=
=
，
∴
=
，即CG•CE=BC•DE．
证明：（1）∵DE∥BC，∴△ADE∽△ABC，△EFG∽△CBG，
∴
| AE |
| AC |
| DE |
| BC |
| EF |
| BC |
| EG |
| CG |
又∵DE=EF，
∴
| DE |
| BC |
| EF |
| BC |
∴
| AE |
| AC |
| EG |
| CG |
（2）∵CF2=FG•FB，
∴
| CF |
| FG |
| FB |
| CF |
又∵∠CFG=∠CFB，
∴△CFG∽△BFC，
∴
| CG |
| BC |
| FG |
| FC |
又∵DF∥BC，
∴∠EFG=∠CBF，
∴∠FCE=∠EFG，
又∵∠FEG=∠CEF，
∴△EFG∽△ECF，
∴
| EF |
| EC |
| FG |
| FC |
| DE |
| EC |
∴
| CG |
| FG |
| DE |
| EC |
点评：本题考查了相似三角形的判定与性质，正确理解相似三角形的判定方法，证明∠FEG=∠CEF，证得△EFG∽△ECF是解决本题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
如图，梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，直线MN为梯形ABCD的对称轴，P为MN上一动点，那么PC+PD的最小值为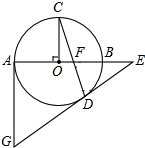
如图，AB是⊙O直径，OC⊥AB，弦CD与OB交于点F，过点D、A分别作⊙O的切线交于点G，切线GD与AB延长线交于点E．
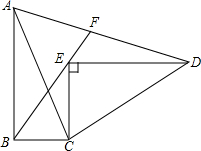Rt△ABC≌Rt△DEC，∠ABC=∠DEC=90°，BE的延长线交AD于点F，求证：AF=DF．