题目内容
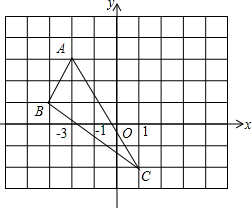 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).(1)直接写出点A、B、C关于y轴对称的点A′、B′、C′坐标:A′(
(2)在x轴上求作一点P,使PA+PB最短.(保留痕迹)
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)根据关于y轴对称点的坐标,纵坐标不变,横坐标改变符号得出答案即可;
(2)作A点关于x轴的对称点A1,连接A1B,与x轴交点即为P;
(2)作A点关于x轴的对称点A1,连接A1B,与x轴交点即为P;
解答:解:(1)A′(2,3),B′(3,1),C′(-1,-2);
(2)如图所示;

(2)如图所示;

点评:本题考查,轴对称-最短路线问题以及坐标与图形的性质,找到关于x轴、y轴的对称点,是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
正多边形的中心角是36°,那么这个正多边形的边数是( )
| A、10 | B、8 | C、6 | D、5 |
已知关于x的方程2x+a=5x-4的解是x=-2,则a的值是( )
| A、-18 | B、-10 |
| C、-6 | D、-2 |
 如图,AB是⊙O的直径,C,P是
如图,AB是⊙O的直径,C,P是
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=
如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=