题目内容
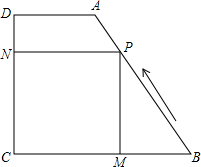 如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=
如图,在梯形ABCD中,AD∥BC,DC⊥BC,AD=2,CD=4,tanB=| 4 |
| 3 |
(1)求AB的长度;
(2)设BP=x,用含x的代数式表示矩形CMPN的面积S.
(3)当点P移动到何位置时,矩形CMPN的面积S取最大值,并求最大值.
考点:相似三角形的判定与性质,二次函数的最值,梯形
专题:
分析:(1)作AE⊥BC于点E,根据正切的定义,即可求得AE和BE的值,然后利用勾股定理即可求解;
(2)根据(1)的解法,利用x表示出PM和CM的长,即可得到函数解析式;
(3)利用二次函数的性质即可求解.
(2)根据(1)的解法,利用x表示出PM和CM的长,即可得到函数解析式;
(3)利用二次函数的性质即可求解.
解答: 解:(1)作AE⊥BC于点E.
解:(1)作AE⊥BC于点E.
则BE=BC-AD=4-2=2,
∵tanB=
,
∴设PM=4y,则BM=3y,则BP=5y.
当AE=CD=4时,4y=4,
则y=1,
则AB=5y=5,BE=3;
(2)BC=AD+BE=2+3=5.
设BP=x,即5y=x,解得:y=
x,PM=
x,BM=
x,
则CM=5-
x,
则S=
x(5-
x),即S=-
x2+4x;
(3)当x=-
=-
=
,则S最大=-
×(
)2+4×
=
.
 解:(1)作AE⊥BC于点E.
解:(1)作AE⊥BC于点E.则BE=BC-AD=4-2=2,
∵tanB=
| 4 |
| 3 |
∴设PM=4y,则BM=3y,则BP=5y.
当AE=CD=4时,4y=4,
则y=1,
则AB=5y=5,BE=3;
(2)BC=AD+BE=2+3=5.
设BP=x,即5y=x,解得:y=
| 1 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
则CM=5-
| 3 |
| 5 |
则S=
| 4 |
| 5 |
| 3 |
| 5 |
| 12 |
| 25 |
(3)当x=-
| b |
| 2a |
| 4 | ||
-
|
| 25 |
| 6 |
| 12 |
| 25 |
| 25 |
| 6 |
| 25 |
| 6 |
| 25 |
| 3 |
点评:本题是二次函数的性质与直角梯形的应用,以及三角函数的定义,正确求得直角△BPM中的三边之间的关系是关键.

练习册系列答案
相关题目
用扑克牌算24点,已抽三张牌为2,4,6,还需抽下面哪张,能算出24( )
| A、K | B、7 | C、Q | D、J |
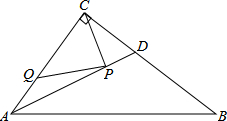 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )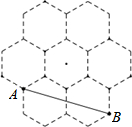 蜂槽的构造非常美丽、科学,如图是由7个形状、大小完全相同的边长为1cm的正六边形组成,则线段AB的长为
蜂槽的构造非常美丽、科学,如图是由7个形状、大小完全相同的边长为1cm的正六边形组成,则线段AB的长为 如图,双曲线y=
如图,双曲线y=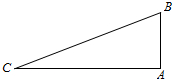 如图,在Rt△ABC中,AB=5,AC=12,∠A=90°.
如图,在Rt△ABC中,AB=5,AC=12,∠A=90°.