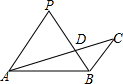
 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
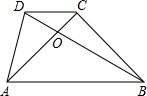 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |
 如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )
如图,若AP=PB,∠APB=2∠ACB,AC与PB交于点D,且PB=5,PD=3,则AD•DC等于( )| A、16 | B、15 | C、7 | D、6 |
 在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )
在四边形ABCD中,AB∥CD,对角线AC、BD交于点O,3CD=2AB,则S△ADC:S△AOB=( )| A、4:9 | B、6:9 |
| C、8:9 | D、10:9 |