题目内容
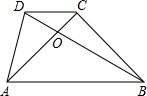在四边形ABCD中，AB∥CD，对角线AC、BD交于点O，3CD=2AB，则S△ADC：S△AOB=（ ）| A、4：9 | B、6：9 |
| C、8：9 | D、10：9 |
考点：相似三角形的判定与性质
专题：
分析：首先根据△AOB∽△COD和3CD=2AB，得到CD：AB=CO：OA=2：3，利用相似三角形的面积的比等于相似比的平方S△COD：S△AOB=4：9，然后利用△COD与△DOA等高，得到S△COD：S△AOD=CO：OA=2：3=4：6，从而求得结论．
解答：解：∵AB∥CD，
∴△AOB∽△COD，
∵3CD=2AB，
∴CD：AB=CO：OA=2：3，
∴S△COD：S△AOB=4：9，
∵△COD与△DOA等高，
∴S△COD：S△AOD=CO：OA=2：3=4：6，
∴S△COD：S△ACD=4：10，
∴S△ADC：S△AOB=10：9．
故选D．
∴△AOB∽△COD，
∵3CD=2AB，
∴CD：AB=CO：OA=2：3，
∴S△COD：S△AOB=4：9，
∵△COD与△DOA等高，
∴S△COD：S△AOD=CO：OA=2：3=4：6，
∴S△COD：S△ACD=4：10，
∴S△ADC：S△AOB=10：9．
故选D．
点评：考查了相似三角形的判定与性质，解题的关键是了解等高的两个三角形的面积的比等于底边的比，难度不大．
练习册系列答案
相关题目
已知，在矩形ABCD中，AB=4，BC=2，点M为边BC的中点，点P为边CD上的动点（点P异于C，D两点）．连接PM，过点P作PM的垂线与射线DA相交于点E（如图），设CP=x，DE=y．
如图，直角梯形ABCD，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60°．以AD为边在直角梯形ABCD外作等边△ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．
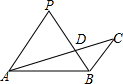如图，若AP=PB，∠APB=2∠ACB，AC与PB交于点D，且PB=5，PD=3，则AD•DC等于（ ）| A、16 | B、15 | C、7 | D、6 |
如图，直线y=
已知：如图，在△ABC中，AB=AC=8cm，BC=6cm，AD平分∠BAC，CE⊥AB交AB于E．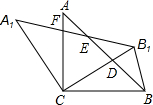
如图，在△ABC中，AC=BC，∠ACB=90°，将△ABC绕点C逆时针旋转α角（0°＜α＜90°），得到△A1B1C，连接BB1，设CB1交AB于D，A1B1分别交AB，AC于E，F